El teorema de Pitàgores relaciona els costats d'un triangle rectangle. Un triangle rectangle és el triangle que té un angle recte ($$90^\circ$$). Als costats que formen l'angle recte se'ls anomena catets, i al costat que queda, hipotenusa. Doncs bé, el teorema de Pitàgores relaciona la hipotenusa amb als seus dos catets. Anem a veure aquesta relació.
Imaginem un triangle rectangle, per exemple de catets $$3$$ i $$4$$ cm i amb una hipotenusa de $$5$$ cm, i dibuixem un quadrat sobre cadascun dels seus costats. Ens queda una figura així:
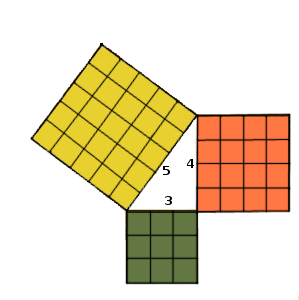
Doncs bé, el sorprenent és que el quadrat de la hipotenusa té la mateixa àrea que els altres dos quadrats junts.
A la nostra imatge de mostra podem comprovar-ho sumant la quantitat de quadradets que conformen cada quadrat. El quadrat de la hipotenusa està format por 25 quadradets, que és igual als 16+9=25 quadradets dels altres dos quadrats.
Aquests valors no són més que l'àrea de cada quadrat, que es calcula $$A_c=costat\cdot costat$$.
$$$5\cdot5=4\cdot4+3\cdot3$$$
$$$5^2=4^2+3^2$$$
$$$25=16+9$$$
$$$25=25$$$
Com podem observar, calcular l'àrea d'un quadrat és elevar al quadrat (elevar a dos) la longitud del catet o hipotenusa en cada cas. Així doncs, podem afirmar que:
En un triangle rectangle el quadrat de la hipotenusa és igual a la suma dels quadrats dels catets.
Aquesta relació es coneix amb el nom de teorema de Pitàgores.
¿I per què es diu així? Doncs perquè els seu descobriment s'atribueix a l'Escola Pitagòrica, fundada per Pitàgores el segle V a.C. i formada per astrònoms, músics, matemàtics i filòsofs que creien que tot es podia expressar mitjançant els nombres. Tot i això, a Mesopotàmia i a l'Antic Egipte ja van utilitzar relacions entre valors, per exemple, dels costats d'un triangle rectangle, però no existeix cap document que contingui explícitament la relació que planteja el teorema de Pitàgores. Tanmateix, la piràmide de Khefren, del segle XXVI a.C. va ser la primera gran piràmide que es va construir basant-se en l'anomenat triangle sagrat egipci, de proporcions 3-4-5, nombres que generen un triangle rectangle i compleixen, per tant, com hem vist en el nostre exemple, el teorema de Pitàgores.
Però el nostre exemple no demostra que aquesta relació sigui certa per a valors qualssevol; és a dir, si considerem un triangle rectangle els catets del qual fan $$b$$ i $$c$$, i la hipotenusa del qual és $$a$$, hem de comprovar que $$$a^2=b^2+c^2$$$
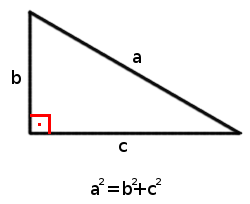
El teorema de Pitàgores compta amb una infinitat de demostracions diferents. De fet el matemàtic estatunidenc Elisha Scott Loomis va publicar el llibre "The Pythagorean Proposition" el 1927 amb 370 demostracions diferents. Loomis classifica les demostracions en quatre apartats: les algebraiques, on es relacionen els costats del triangle; geomètriques, en les que es comparen àrees; dinàmiques, a través de les propietats de força i massa; i les quaterniòniques, que usen els vectors. En aquesta unitat només farem una demostració geomètrica.
Demostració geomètrica del teorema de Pitàgores
Partim del triangle rectangle genèric representat abans per enunciar el teorema. Llavors, construim un quadrat el costat del qual mesuri la suma dels catets, és a dir, un quadrat de costat $$(b+c)$$. Estarem d'acord que l'àrea d'aquest quadrat és $$(b+c)^2$$.

Hem posat les mides de $$b$$ i $$c$$ de tal forma que si tracem les hipotenuses construim quatre triangles rectangles com el genèric, quedant un quadrat intern de costat $$a$$.
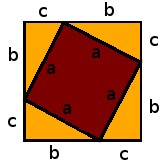
Ara podem escriure l'àrea del quadrat gran, que abans hem calculat com a $$(b+c)^2$$, però fent la suma de les àrees dels quatre triangles més el quadrat intern.
Tenim quatre triangles rectangles d'àrea $$A_t=\dfrac{b\cdot c}{2}$$ i un quadrat d'àrea $$a^2$$. Ens queda doncs la següent igualtat:
$$$4\cdot\dfrac{b\cdot c}{2}+a^2 = (b+c)^2$$$
Ho desenvolupem als dos costats:
$$$2\cdot b\cdot c + a^2 = b^2+2\cdot b \cdot c + c^2$$$
$$$2\cdot b\cdot c + a^2 - 2\cdot b \cdot c= b^2 + c^2$$$
$$$a^2= b^2 + c^2$$$
Amb la qual cosa acabem d'obtenir la relació que enuncia el teorema de Pitàgores.
També ens podem trobar enunciats del teorema de Pitàgores en els que s'utilitzen altres lletres/variables per expressar la igualtat. Així, si anomenem $$h$$ a la hipotenusa i $$c_1$$ i $$c_2$$ als dos catets, ens queda
$$$h^2=c_1^2+c_2^2$$$
El que és important és saber quina lletra identifica a cada cosa.
Aplicacions
La relació que ens enuncia el teorema de Pitàgores ens permet trobar la longitud de qualsevol dels costats d'un triangle rectangle donades les longituds dels altres dos.
Així, recordant que si els catets fan $$b$$ i $$c$$, i la hipotenusa fa $$a$$, de la relació $$a^2=b^2+c^2$$ deduïm aquestes tres igualtats:
$$$a = \sqrt{b^2 + c^2}$$$
$$$b = \sqrt{a^2-c^2}$$$
$$$c = \sqrt{a^2 - b^2}$$$
Vegem uns exemples en un parell de triangles rectangles en els que haurem de trobar la longitud que ens falta d'un costat del triangle.
El següent triangle rectangle té uns catets que fan $$12$$ i $$16$$ unitats, doncs són els costats que formen l'angle recte.
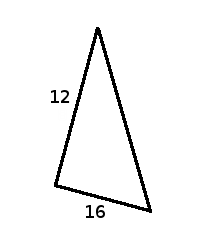
Per trobar la hipotenusa n'hi ha prou amb recordar el teorema de Pitàgores, $$a^2=b^2+c^2$$. Doncs aillant la $$a$$ que representa a la hipotenusa ens queda
$$$a=\sqrt{b^2 + c^2}=\sqrt{12^2 + 16^2}=\sqrt{144+256}=\sqrt{400}=20$$$
Així doncs, ja sabem que la hipotenusa d'aquest triangle rectangle fa $$20$$ unitats.
Vegem què passa amb un altre triangle rectangle.
En aquest cas coneixem la longitud d'un catet i de la hipotenusa.
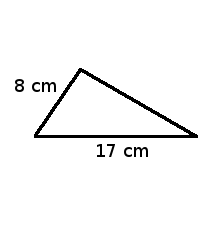
En concret, un catet, podem considerar-lo el $$b$$ o el $$c$$ indistintament, fa $$8$$cm i la hipotenusa fa $$a=17$$cm.
Per trobar el catet que ens falta utilitzem el teorema de Pitàgores, $$a^2=b^2+c^2$$, i hem d'aillar la variable $$c$$:
$$$c^2=a^2-b^2 \Rightarrow c=\sqrt{a^2 - b^2}=\sqrt{17^2 - 8^2}=\sqrt{289-64}=\sqrt{225}=15$$$
Per tant, el catet que ens faltaba fa $$15$$cm.
Per acabar la unitat resoldrem aquest problema que ens hem inventat.
Volem construir un estel per jugar-hi aquest cap de setmana. Per tant hem de comprar uns llistons fins de fusta i tela de colors. Sabem les dimensions de les diagonals que formen l'estel.

¿Quants centímetres de llistó de fusta i quants metres quadrats de tela necessitem?
Com podem observar en el dibuix que hem fet del nostre estel, ens cal saber les mides de les vores de fusta de l'estel.
Si ens hi fixem, les dues diagonals formen quatre triangles rectangles, iguals dos a dos. El petit està format per dos catets de $$22$$ i $$30$$ cm, i el gran està format por dos catets de $$65$$ i $$22$$ cm respectivament. Hem de trobar què fan de llarg les dues hipotenuses. Per a això, utilitzem el teorema de Pitàgores.
Anomenem $$a$$ a la hipotenusa del triangle rectangle petit, i $$b$$ i $$c$$ als dos catets:
$$$a^2=b^2+c^2$$$
$$$a=\sqrt{b^2 + c^2}=\sqrt{30^2 + 22^2}=\sqrt{900+484}=\sqrt{1384}\approx 37,2$$$
Ja sabem que la hipotenusa petita fa $$37,2$$ cm.
Ara anomenem $$A$$ a la hipotenusa del triangle rectangle gran, i $$B$$ i $$C$$ als dos catets:
$$$A^2=B^2+C^2$$$
$$$A=\sqrt{B^2 + C^2}=\sqrt{65^2 + 22^2}=\sqrt{4225+484}=\sqrt{4709}\approx 68,6$$$
Per tant, la hipotenusa gran fa $$68,6$$ cm.
Sumem ara totes les longituds dels llistons de fusta que necessitem. Primer sumarem les diagonals i després les vores de l'estel:
$$$65+30+(2\cdot22)=139$$$
$$$(2\cdot37,2)+(2\cdot68,6)=211,6$$$
Així doncs necessitem $$139+211,6=350,6$$ cm de llistó fi de fusta.
Ara només ens cal calcular la superfície dels quatre triangles. Per a això, recordem que l'àrea d'un triangle és $$A=\dfrac{\text{base·altura}}{2}$$.
Anomenem $$A_p$$ a l'àrea del triangle rectangle petit i $$A_g$$ a la del gran.
$$$A_p=\dfrac{22\cdot30}{2}=330 \ cm^2$$$
$$$A_g=\dfrac{22\cdot65}{2}=715 \ cm^2$$$
Però tenim dos triangles de cada. Per tant hem de multiplicar per dos, i finalment sumar-ho tot:
$$$A_{total}=(330\cdot2)+(715\cdot2)=2090 \ cm^2$$$
Així, quan anem a comprar la tela, podem demanar un quadrat de tela de $$\sqrt{2090}\approx 46$$ cm de costat.
