Pythagorean theorem

The Pythagorean theorem describes the relationship of the sides of a right triangle. A right triangle is a triangle with a right angle ( $90^{\circ}$ ). The sides forming the right angle are called catheti or legs and the remaining side the hypotenuse. The Pythagorean theorem relates the hypotenuse with the two legs. Let's explore this relationship!

Let's imagine a triangle which legs measure $3$ y $4$ cm and a hypotenuse of $5$ cm, and draw a square on each of its sides. We will get a figure like this:

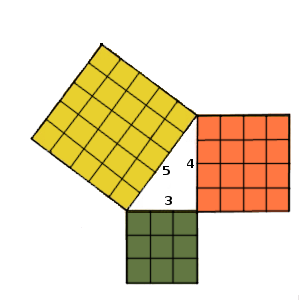
imagen

Well, what is surprising is that the square of the hypotenuse is the same area as the other two squares together.

In our sample image, we can check this by adding the number of the little squares that make up each square, and comparing the number of squares with those of the hypotenuse which has 25 squares: 16 +9 = 25

To calculate this we use the following formula: $A_{c} = l a d o \cdot l a d o$ .

$5 \cdot 5 = 4 \cdot 4 + 3 \cdot 3$

$5^{2} = 4^{2} + 3^{2}$

$25 = 16 + 9$

$25 = 25$

As we can see, to calculate the area of the squares, we square (to two) the length of each leg and the hypotenuse. Thus, we can state that:

In a right triangle the square of the hypotenuse equals the sum of the squares of the legs.

This relationship is known by the Pythagorean theorem.

Why? Well, because its discovery is attributed to the Pythagorean school founded by Pythagoras in the 5th century BC and formed by astronomers, musicians, mathematicians and philosophers who believed that everything could be expressed in numbers. Already in Mesopotamia and Ancient Egypt values were related as, for example, the sides of a right triangle. But there is no document which explicitly contains the relationship posed the Pythagorean theorem. However, the Pyramid of Khafre from the 16th century A.C. was the first big pyramid that was built based on the so-called sacred Egyptian triangle with the proportions 3-4-5, numbers that generate a right triangle and meet therefore, as we have seen in our example, the Pythagorean theorem .

But our example does not show that this relationship is true for all values, i.e., if we consider a right triangle which legs measure $b$ and $c$ , and a hypotenuse of $a$ , we have to check that $a^{2} = b^{2} + c^{2}$

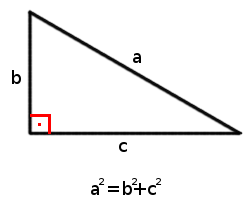
imagen

The Pythagorean theorem has an infinity of different proofs, in fact, the American mathematician Elisha Scott Loomis published the book "The Pythagorean Proposition" in 1927 with 370 different proofs. Loomis classified the proofs into four sections: algebraic, where the sides of the triangle are related; geometric, in which areas are compared; dynamic, through the properties of strength and mass; and quaternionic, using vectors. In this unit we will do a geometric proof.

Geometric Proof of the Pythagorean Theorem

We start from the generic right triangle introduced above to state the theorem. Then, we construct a square with a side measure that equals the sum of the legs, i.e., a square on the side $(b + c)$ . We will agree that the area of this square is $(b + c)^{2}$ .

imagen

We have arranged the measures $b$ and $c$ in a way that, if we draw the hypotenuses, we construct four right triangles like the generic one, leaving an inner square on the side $a$ .

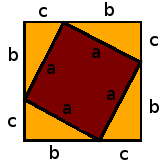
imagen

Now we can write the area of the large square, which we have previously calculated as $(b + c)^{2}$ , by using the sum of the areas of the four triangles plus the inner square.

We have four right triangles with an area $A_{t} = \frac{b \cdot c}{2}$ and a square with the area $a^{2}$ . Thus, we get to the following equality:

$4 \cdot \frac{b \cdot c}{2} + a^{2} = (b + c)^{2}$

Let's develop both sides:

$2 \cdot b \cdot c + a^{2} = b^{2} + 2 \cdot b \cdot c + c^{2}$

$2 \cdot b \cdot c + a^{2} - 2 \cdot b \cdot c = b^{2} + c^{2}$

$a^{2} = b^{2} + c^{2}$

Like this we get the relationship stated by the Pythagorean theorem.

We can also find statements of the Pythagorean theorem using other letters/variables to express equality. Let's see, if we assign $h$ to the hypotenuse and $c_{1}$ and $c_{2}$ to the two legs we get

$h^{2} = c_{1}^{2} + c_{2}^{2}$

The important point is to know which letter stands for what.

Applications

The relationship stated by the Pythagorean theorem allows us to find the length of any side of a right triangle, if we have the lengths of the other two sides.

Let's review: if the legs are $b$ and $c$ , and the hypotenuse is $a$ , we can deduce the following three equalities from the relation $a^{2} = b^{2} + c^{2}$ :

$a = \sqrt{b^{2} + c^{2}}$

$b = \sqrt{a^{2} - c^{2}}$

$c = \sqrt{a^{2} - b^{2}}$

Let's look at some right triangles and find the length of the one side we don't have.

Example

The legs of the following right triangle measure $12$ and $16$ units and are the sides that form the right angle.

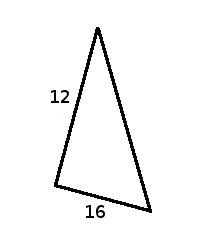
imagen

To find the hypotenuse we just need to remember the Pythagorean theorem, $a^{2} + b^{2} = c^{2}$ , thus isolating $a$ which represents the hypotenuse we get

$a = \sqrt{b^{2} + c^{2}} = \sqrt{12^{2} + 16^{2}} = \sqrt{144 + 256} = \sqrt{400} = 20$

Thus, we know that the hypotenuse of this right triangle measures $20$ units.

Let's see what happens with another triangle.

Example

In this case we know the length of one leg and the hypotenuse.

imagen

We can assign either $b$ or $c$ to the leg, it measures $8$ cm and the hypotenuse $a = 17$ cm.

To find the length of the other leg we use the Pythagorean theorem, $a^{2} + b^{2} = c^{2}$ , and isolate the variable $c$ :

$c^{2} = a^{2} - b^{2} \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{17^{2} - 8^{2}} = \sqrt{289 - 64} = \sqrt{225} = 15$

Therefore the missing leg measures $15$ cm.

To end the unit, let's solve this invented problem.

Example

We want to build a kite to go kite flying this weekend. What we need are thin sticks of wood and colourful fabric. We know the dimensions of the diagonals of the comet.

imagen

How long do the wooden sticks have to be and how many square meters of fabric do we need?

As seen in the picture we have of our kite, we need to know the measures of the wooden edges of the kite.

If you look closely, the two diagonals form four right triangles, with two and two being equal. The legs of the small one measure $22$ and $30$ cm, and the legs of the large one $65$ and $22$ cm respectively. What we need know is the length of the two hypotenuses. To calculate this, we use the Pythagorean theorem.

We assign $a$ to the hypotenuse of the small right triangle, and $b$ and $c$ to the two legs:

$a^{2} = b^{2} + c^{2}$

$a = \sqrt{b^{2} + c^{2}} = \sqrt{30^{2} + 22^{2}} = \sqrt{900 + 484} = \sqrt{1384} \approx 37, 2$

We now know that the small hypotenuse measures $37.2$ cm.

Now we assign $A$ to the hypotenuse of the large right triangle, and $B$ and $C$ to the two legs:

$A^{2} = B^{2} + C^{2}$

$A = \sqrt{B^{2} + C^{2}} = \sqrt{65^{2} + 22^{2}} = \sqrt{4225 + 484} = \sqrt{4709} \approx 68, 6$

Thus, the large hypotenuse measures $68.6$ cm.

Let's add all the lengths of the wooden sticks we need. First we add the diagonals and then the edges of the kite:

$65 + 30 + (2 \cdot 22) = 139$

$(2 \cdot 37, 2) + (2 \cdot 68, 6) = 211, 6$

We need a total of $139 + 211, 6 = 350, 6$ cm of thin wooden sticks.

Now we only need to calculate the surface area of the four triangles. To do this, we remember that the area of a triangle is $A = \frac{base·height}{2}$ .

We assign $A_{p}$ to the small right triangle and $A_{g}$ to the big one.

$A_{p} = \frac{22 \cdot 30}{2} = 330 c m^{2}$

$A_{g} = \frac{22 \cdot 65}{2} = 715 c m^{2}$

But attention! We have two triangles each, so we have to multiply by two, and finally add it all up:

$A_{t o t a l} = (330 \cdot 2) + (715 \cdot 2) = 2090 c m^{2}$

So, when shopping for fabric, we need to get a square of fabric with a side measure of $\sqrt{2090} \approx 46$ cm.