Teorema de Pitágoras

El teorema de Pitágoras relaciona los lados de un triángulo rectángulo. Un triángulo rectángulo es el triángulo que tiene un ángulo recto ( $90^{\circ}$ ). A los lados que forman el ángulo recto se les llama catetos y al lado restante hipotenusa. Pues bien, el teorema de Pitágoras relaciona la hipotenusa con sus dos catetos. Vamos ahora a descubrir esta relación.

Imaginemos un triángulo rectángulo, por ejemplo de catetos $3$ y $4$ cm y con una hipotenusa de $5$ cm, y dibujamos un cuadrado sobre cada uno de sus lados. Nos queda una figura así:

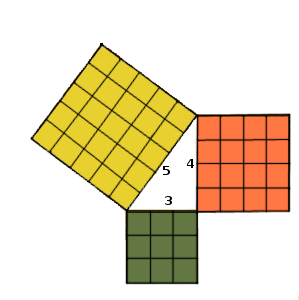
imagen

Pues bien, lo sorprendente es que el cuadrado de la hipotenusa tiene la misma área que los otros dos cuadrados juntos.

En nuestra imagen de muestra podemos comprobarlo sumando la cantidad de cuadraditos que conforman cada cuadrado, pues, el cuadrado de la hipotenusa está formado por 25 cuadraditos, que es igual a los 16+9=25 cuadraditos de los otros dos cuadrados.

Estos valores no son más que el área de cada cuádrado, que se calcula $A_{c} = l a d o \cdot l a d o$ .

$5 \cdot 5 = 4 \cdot 4 + 3 \cdot 3$

$5^{2} = 4^{2} + 3^{2}$

$25 = 16 + 9$

$25 = 25$

Como podemos observar, calcular el área de un cuadrado es elevar al cuadrado (elevar a dos) la longitud del cateto o hipotenusa en cada caso. Así pues, podemos afirmar que:

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Esta relación se conoce con el nombre de teorema de Pitágoras.

¿Y por qué se llama así? Pues porqué su descubrimiento se atribuye a la Escuela Pitagórica, fundada por Pitágoras el siglo V a.C. y formada por astrónomos, músicos, matemáticos y filósofos que creían que todo podía expresarse mediante números. Aún así, en Mesopotamia y el Antiguo Egipto ya utilizaron relaciones entre valores, por ejemplo, de los lados de un triángulo rectángulo, pero no existe ningún documento que contenga explícitamente la relación que plantea el teorema de Pitágoras. Sin embargo, la pirámide de Kefrén, del siglo XXVI a.C. fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5, números que generan un triángulo rectángulo y cumplen, por lo tanto, como hemos visto en nuestro ejemplo, el teorema de Pitágoras.

Pero nuestro ejemplo no demuestra que esta relación sea cierta para valores cualesquiera, es decir, si consideramos un triángulo rectángulo cuyos catetos miden $b$ y $c$ , y cuya hipotenusa es $a$ , tenemos que comprobar que $a^{2} = b^{2} + c^{2}$

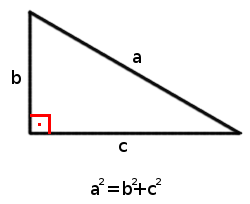
imagen

El teorema de Pitágoras cuenta con una infinidad de demostraciones diferentes, de hecho el matemático estadounidense Elisha Scott Loomis publicó el libro "The Pythagorean Proposition" en 1927 con 370 demostraciones diferentes. Loomis clasifica las demostraciones en cuatro apartados: las algebraicas, donde se relacionan los lados del triángulo; geométricas, en las que se comparan áreas; dinámicas, a través de las propiedades de fuerza y masa; y las cuaterniónicas, que usan los vectores. En esta unidad solamente haremos una demostración geométrica.

Demostración geométrica del teorema de Pitágoras

Partimos del triángulo rectángulo genérico representado anteriormente para enunciar el teorema. Entonces, construimos un cuadrado cuyo lado mida la suma de los catetos, es decir, un cuadrado de lado $(b + c)$ . Estaremos de acuerdo que el área de este cuadrado es $(b + c)^{2}$ .

imagen

Hemos puesto las medidas de $b$ y $c$ de tal forma que si trazamos las hipotenusas construimos cuatro triángulos rectángulos como el genérico, quedando un cuadrado interno de lado $a$ .

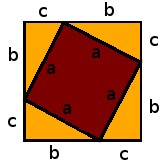
imagen

Ahora podemos escribir el área del cuadrado grande, que antes hemos calculado como $(b + c)^{2}$ , pero haciendo la suma de las áreas de los cuatro triángulos más el cuadrado interno.

Tenemos cuatro triángulos rectángulos de área $A_{t} = \frac{b \cdot c}{2}$ y un cuadrado de área $a^{2}$ . Nos queda pues la siguiente igualdad:

$4 \cdot \frac{b \cdot c}{2} + a^{2} = (b + c)^{2}$

Desarrollamos a los dos lados:

$2 \cdot b \cdot c + a^{2} = b^{2} + 2 \cdot b \cdot c + c^{2}$

$2 \cdot b \cdot c + a^{2} - 2 \cdot b \cdot c = b^{2} + c^{2}$

$a^{2} = b^{2} + c^{2}$

Con lo que acabamos de obtener la relación que enuncia el teorema de Pitágoras.

También nos podemos encontrar enunciados del teorema de Pitágoras en los que utilizan otras letras/variables para expresar la igualdad. Así, si llamamos $h$ a la hipotenusa y $c_{1}$ y $c_{2}$ a los dos catetos nos queda

$h^{2} = c_{1}^{2} + c_{2}^{2}$

Lo importante es saber qué letra significa qué.

Aplicaciones

La relación que nos enuncia el teorema de Pitágoras nos permite encontrar la longitud de cualesquiera de los lados de un triángulo ¡rectángulo! dadas las longitudes de los otros dos.

Así, recordando que si los catetos miden $b$ y $c$ , y la hipotenusa mide $a$ , de la relación $a^{2} = b^{2} + c^{2}$ deducimos estas tres igualdades:

$a = \sqrt{b^{2} + c^{2}}$

$b = \sqrt{a^{2} - c^{2}}$

$c = \sqrt{a^{2} - b^{2}}$

Vamos a ver unos ejemplos en un par de triángulos rectángulos en los que tendremos que encontrar la longitud que nos falta de un lado del triángulo.

Ejemplo

El siguiente triángulo rectángulo tiene unos catetos que miden $12$ y $16$ unidades, pues son los lados que forman el ángulo recto.

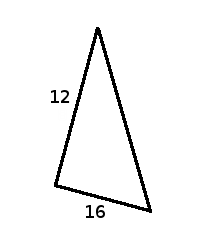
imagen

Para encontrar la hipotenusa basta con recordar el teorema de Pitágoras, $a^{2} = b^{2} + c^{2}$ , pues aislando la $a$ que representa a la hipotenusa nos queda

$a = \sqrt{b^{2} + c^{2}} = \sqrt{12^{2} + 16^{2}} = \sqrt{144 + 256} = \sqrt{400} = 20$

Así pues, ya sabemos que la hipotenusa de este triángulo rectángulo mide $20$ unidades.

Veamos qué sucede con otro triángulo rectángulo.

Ejemplo

En este caso conocemos la longitud de un cateto y de la hipotenusa.

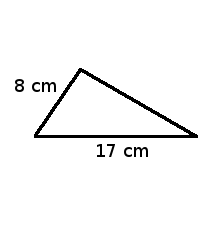
imagen

En concreto, un cateto, podemos considerarlo el $b$ o el $c$ indistintamente, mide $8$ cm y la hipotenusa mide $a = 17$ cm.

Para encontrar el cateto que nos falta utilizamos el teorema de Pitágoras, $a^{2} = b^{2} + c^{2}$ , y tenemos que aislar la variable $c$ :

$c^{2} = a^{2} - b^{2} \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{17^{2} - 8^{2}} = \sqrt{289 - 64} = \sqrt{225} = 15$

Con lo que el cateto que nos faltaba mide $15$ cm.

Para finalizar la unidad vamos a resolver este problema que nos hemos inventado.

Ejemplo

Queremos construir una cometa para jugar con ella este fin de semana. Para ello tenemos que ir a comprar listones finos de madera y tela de colores. Sabemos las dimensiones de las diagonales que conforman la cometa.

imagen

¿Cuántos centímetros de listón de madera y cuántos metros cuadrados de tela necesitamos?

Como podemos observar en el dibujo que hemos hecho de nuestra cometa, necesitamos saber lo que miden los bordes de madera de la cometa.

Si nos fijamos, las dos diagonales forman cuatro triángulos rectángulos, iguales dos a dos. El pequeño está formado por dos catetos de $22$ y $30$ cm, y el grande está formado por dos catetos de $65$ y $22$ cm respectivamente. Tenemos que hallar cuánto miden las dos hipotenusas. Para ello, utilizamos el teorema de Pitágoras.

Llamamos $a$ a la hipotenusa del triángulo rectángulo pequeño, y $b$ y $c$ los dos catetos:

$a^{2} = b^{2} + c^{2}$

$a = \sqrt{b^{2} + c^{2}} = \sqrt{30^{2} + 22^{2}} = \sqrt{900 + 484} = \sqrt{1384} \approx 37, 2$

Ya sabemos que la hipotenusa pequeña mide $37, 2$ cm.

Ahora llamamos $A$ a la hipotenusa del triángulo rectángulo grande, y $B$ y $C$ los dos catetos:

$A^{2} = B^{2} + C^{2}$

$A = \sqrt{B^{2} + C^{2}} = \sqrt{65^{2} + 22^{2}} = \sqrt{4225 + 484} = \sqrt{4709} \approx 68, 6$

Con lo que la hipotenusa grande mide $68, 6$ cm.

Sumemos pues ahora todas las longitudes de los listones de madera que necesitamos. Primero sumaremos las diagonales y luego los bordes de la cometa:

$65 + 30 + (2 \cdot 22) = 139$

$(2 \cdot 37, 2) + (2 \cdot 68, 6) = 211, 6$

Así pues necesitamos $139 + 211, 6 = 350, 6$ cm de listón fino de madera.

Ahora solamente nos falta calcular la superfície de los cuatro tríangulos. Para eso, recordamos que el área de un triángulo es $A = \frac{base·altura}{2}$ .

Llamamos $A_{p}$ al área del triángulo rectángulo pequeño y $A_{g}$ a la del grande.

$A_{p} = \frac{22 \cdot 30}{2} = 330 c m^{2}$

$A_{g} = \frac{22 \cdot 65}{2} = 715 c m^{2}$

Pero tenemos dos triángulos de cada, con lo que tenemos que multiplicar por dos, y finalmente sumarlo todo:

$A_{t o t a l} = (330 \cdot 2) + (715 \cdot 2) = 2090 c m^{2}$

Así, para ir a comprar la tela, podemos pedir un cuadrado de tela de $\sqrt{2090} \approx 46$ cm de lado.