Anem a aprendre a crear i resoldre un ítem del següent tipus (més complicats que aquest sens dubte que també):
Un fuster ha de construir taules rectangulars els costats de les quals no sobrepassin $$2$$ metres i tals que la suma del seu costat major i el doble del menor no sobrepassi $$4$$ metres. Quin és el màxim valor del perímetre d'aquestes taules?
En aquest tipus de problemes, apareix certa quantitat que s'ha de maximitzar (també podria ser minimitzar, però no és aquest el cas). En aquest exemple és el perímetre de les taules, que està subjecte a certes restriccions. La funció a maximitzar(o minimitzar) s'anomena funció objectiu. El valor màxim (o mínim) de la funció objectiu es troba a les vores de la zona factible delimitada per les restriccions del problema. A aquest valor s'anomena valor òptim.
Vegem com expressar el problema de l'exemple matemàticament:
El primer a identificar són les variables o incògnites. En aquest cas seran el costat llarg de la taula (al qual anomenarem $$x$$) i el costat curt de la taula (al qual anomenarem $$y$$).
Identifiquem la funció objectiu. Què se'ns demana maximitzar / minimitzar? Com s'expressa aquesta quantitat en funció de les variables del problema?
En el nostre cas se'ns demana maximitzar el perímetre (al qual anomenarem $$P$$) de les taules. El perímetre es pot expressar com a funció de les variables del problema (costat llarg i costat curt), ja que és directament la suma del doble de cada costat. Matemàticament: $$$P(x,y)=2x+2y$$$
Escrivim les restriccions com inequacions. Aquestes restriccions són:
-
Els costats no poden ser de més de dos metres (ni de menys de zero, ja que no tindria sentit): $$$ x\geqslant 0 \qquad x\leqslant 2 \qquad y\geqslant 0 \qquad y\leqslant 2 $$$
- La suma del costat major i el doble de la menor no ha de sobrepassar els $$4$$ metres: $$$ x+ 2y\leqslant 4$$$
Identifiquem la regió de validesa definida per les restriccions i calculem els vèrtexs d'aquesta regió. Les rectes associades a les restriccions són:
- $$x=0$$ i $$x=2$$, que són rectes paral.leles a l'eix $$y$$, que passen per $$x=0$$ i $$x=2$$ respectivament. Les desigualtats que provenen defineixen una franja de solucions factibles entre $$x=0$$ i $$x=2$$.
- $$y=0$$ i $$y=2$$, que són rectes paral.leles a l'eix $$x$$, que passen per $$y=0$$ i $$y=2$$ respectivament. Les desigualtats que provenen defineixen una franja de solucions factibles entre $$y=0$$ i $$y=2$$.
- $$y=-\dfrac{1}{2}x+2$$, la zona de validesa està per sota de la recta (es pot veure comprovant que el punt $$(0,0)$$, que està per sota de la recta, compleix la inequació $$x+2y\leqslant 4$$).
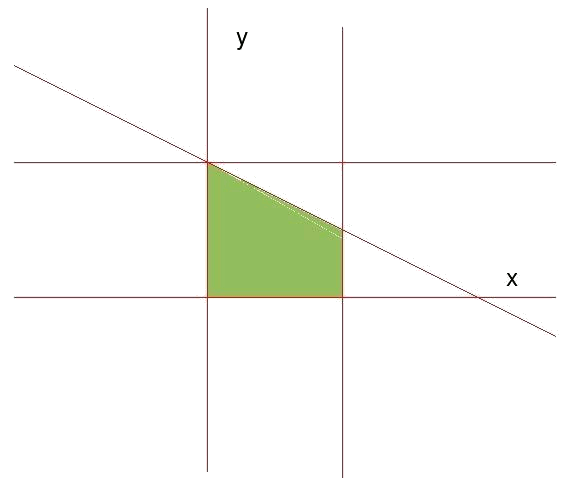
Els vèrtexs de la regió de validesa es calculen veient en quins punts es tallen les rectes definides per les restriccions i després seleccionant d'aquests punts els que compleixen totes les inequacions. Fent això veiem que els vèrtexs de la regió de validesa tenen per coordenades:
-
$$(0,0)$$ on tallen $$x=0$$ i $$y=0$$.
-
$$(2,0)$$ on tallen $$x=2$$ i $$y=0$$.
-
$$(2,1)$$ on tallen $$x=2$$ i $$y=-\dfrac{1}{2}x+2$$.
- $$(0,2)$$ on tallen $$x=0$$ i $$y=-\dfrac{1}{2}x+2$$.
L'últim pas és calcular el valor de la funció objectiu en els vèrtexs de la regió de validesa, per veure quin dels punts maximitza el perímetre de les taules.
- $$P(0,0)=2\cdot 0+2\cdot 0=0$$
- $$P(2,0)=2\cdot 2+2\cdot 0=4$$
- $$P(2,1)=2\cdot 2+2\cdot 1=6$$
- $$P(0,2)=2\cdot 0+2\cdot 2=4$$
Veiem que el perímetre es maximitza al punt $$(2,0)$$. La funció perímetre presa allà el seu valor òptim, que és $$6$$ metres. Les coordenades del punt ens estan dient que maximitzarà el perímetre fent taules de costat llarg ($$x$$) de $$2$$ metres i costat curt ($$y$$) d'$$1$$ metre. Ja hem resolt el primer problema complet de programació lineal.
Altres exemples:
Els $$400$$ alumnes d'una escola aniran d'excursió. Per a això es contracta el viatge a una empresa que disposa de $$8$$ autobusos del tipus A amb $$40$$ places i $$10$$ del tipus B amb $$50$$ places, però només de $$9$$ conductors per a aquest dia. Donada la diferent capacitat i qualitat, el lloguer de cada autobús dels grans (tipus B) costa $$80$$ € i el de cada un dels petits (tipus A), $$60$$ €. Quants autobusos de cada classe caldrà llogar perquè el viatge resulti el més econòmic possible?
Primer identifiquem les variables. En aquest cas seran el nombre d'autobusos del tipus A (al qual anomenarem $$x$$) i el nombre d'autobusos del tipus B (al qual anomenarem $$y$$). La funció objectiu és el preu i s'ha de minimitzar. El preu en funció de les variables del problema serà la suma del que val un autobús del tipus A (a $$60$$ €) multiplicat pel nombre d'autobusos del tipus A que es lloguen més el mateix, però dels autobusos tipus B (a $$80$$ €). És a dir, el preu serà: $$$P(x,y)=60\cdot x+80\cdot y$$$
Les restriccions del problema en forma d'inequacions:
-
$$x\geqslant 0$$, $$y\geqslant 0$$ (per lògica, no podem llogar un nombre negatiu d'autobusos).
-
$$x\leqslant 8$$ (només hi ha $$8$$ autobusos del tipus A).
-
$$y\leqslant 10$$ (només hi ha $$10$$ autobusos del tipus B).
-
$$x+y\leqslant 9$$ (només hi ha $$9$$ conductors).
- $$40\cdot x +50\cdot y\geqslant 400$$ (volem que el nombre total de places d'autobús disponibles sigui com a mínim igual al nombre d'alumnes).
Busquem les rectes associades a les inequacions, les zones de validesa de cada inequació i la zona factible comuna a totes les restriccions.
I la zona factible queda:
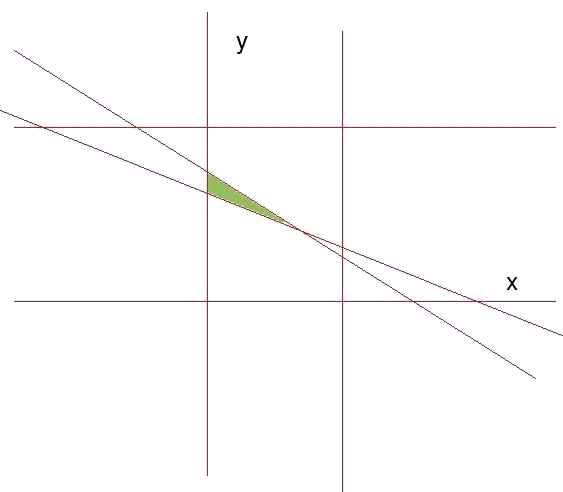
El següent pas és calcular els vèrtexs de la regió de validesa. En aquest cas són: $$$ (0,8) \qquad (0,9) \qquad (5,4)$$$
La funció objectiu (el preu) pren els següents valors en els vèrtexs de la regió de solucions factibles:
- $$P(0,8)=60\cdot 0+80\cdot 8=640$$ €
- $$P(0,9)=60\cdot 0+80\cdot 9=720$$ €
- $$P(5,4)=60\cdot 5+80\cdot 4=620$$ €
com volem minimitzar el preu, el punt que volem és el $$(5,4)$$ i el preu pren el valor de $$620$$ €. Per tant, minimitzant el preu si es lloguen $$5$$ autobusos del tipus A ($$x$$) i $$4$$ autobusos del tipus B ($$y$$) i tot sortirà per $$620$$ €.
En resum, en tot problema de programació lineal haurem de seguir els mateixos passos:
- Triar les variables del problema.
- Escriure la funció objectiu en funció de les dades del problema.
- Escriure les restriccions en forma d'inequacions.
- Determinar la regió factible que indiquen les restriccions.
- Calcular les coordenades dels vèrtexs de la regió de solucions factibles.
- Calcular el valor de la funció objectiu en cadascun dels vèrtexs per veure en quin d'ells presenta el major màxim o mínim, segons ens demani el problema.
