Vamos a aprender a crear y resolver un ejercicio del siguiente tipo (más complicados que este sin duda que también):
Un carpintero tiene que construir mesas rectangulares cuyos lados no sobrepasen $$2$$ metros y tales que la suma de su lado mayor y el doble de la menor no sobrepase $$4$$ metros. ¿Cuál es el máximo valor del perímetro de dichas mesas?
En este tipo de problemas, aparece cierta cantidad que se ha de maximizar (también podría ser minimizar, pero no es este el caso). En este ejemplo es el perímetro de las mesas, que está sujeto a ciertas restricciones. La función a maximizar ( minimizar ) se lama función objetivo. El valor máximo (o mínimo) de la función objetivo se halla en los bordes de la zona factible delimitada por las restricciones del problema. A este valor se le llama el valor óptimo.
Veamos cómo expresar el problema del ejemplo matemáticamente:
Igual que en el primer nivel, lo primero a identificar son las variables o incógnitas. En este caso serán el lado largo de la mesa (al que llamaremos $$x$$) y el lado corto de la mesa (al que llamaremos $$y$$).
Identificamos la función objetivo. ¿Qué se nos pide maximizar/minimizar? y ¿Cómo se expresa esta cantidad en función de las variables del problema?
En nuestro caso se nos pide maximizar el perímetro (al que llamaremos $$P$$) de las mesas. El perímetro se puede expresar como función de las variables del problema (lado largo y lado corto), ya que es directamente la suma del doble de cada lado. Matemáticamente: $$$P(x,y)=2x+2y$$$
Escribimos las restricciones como inecuaciones. Estas restricciones son:
-
Los lados no pueden ser de más de dos metros (ni de menos de cero, ya que no tendría sentido): $$$ x\geqslant 0 \qquad x\leqslant 2 \qquad y\geqslant 0 \qquad y\leqslant 2 $$$
- La suma del lado mayor y el doble de la menor no ha de sobrepasar los $$4$$ metros: $$$ x+ 2y\leqslant 4$$$
Identificamos la región de validez definida por las restricciones y calculamos los vértices de dicha región. Las rectas asociadas a las restricciones son:
- $$x=0$$ y $$x=2$$, que son rectas paralelas al eje $$y$$, que pasan por $$x=0$$ y $$x=2$$ respectivamente. Las desigualdades de que provienen definen una franjade soluciones factibles entre $$x=0$$ y $$x=2$$.
- $$y=0$$ y $$y=2$$, que son rectas paralelas al eje $$x$$, que pasan por $$y=0$$ y $$y=2$$ respectivamente. Las desigualdades de que provienen definen una franjade soluciones factibles entre $$y=0$$ y $$y=2$$.
- $$y=-\dfrac{1}{2}x+2$$, cuya zona de validez está por debajo de la recta (se puede ver comprobando que el punto $$(0,0)$$, que está por debajo de la recta, cumple la inecuación $$x+2y\leqslant 4$$).
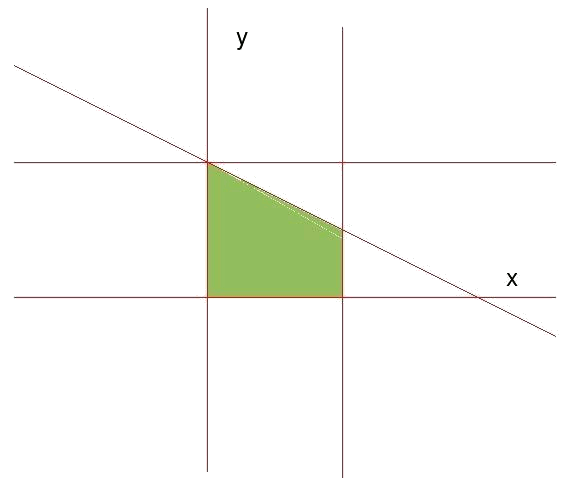
Los vértices de la región de validez se calculan como en el nivel anterior: viendo en qué puntos se cortan las rectas definidas por las restricciones y luego seleccionar de estos puntos los que cumplen todas las inecuaciones. Haciendo esto vemos que los vertices de la región de validez tienen por coordenadas:
-
$$(0,0)$$ donde cortan $$x=0$$ e $$y=0$$.
-
$$(2,0)$$ donde cortan $$x=2$$ e $$y=0$$.
-
$$(2,1)$$ donde cortan $$x=2$$ e $$y=-\dfrac{1}{2}x+2$$.
- $$(0,2)$$ donde cortan $$x=0$$ e $$y=-\dfrac{1}{2}x+2$$.
El último paso es calcular el valor de la función objetivo en los vértices de la región de validez, para ver cual de los puntos maximiza el perímetro de las mesas.
- $$P(0,0)=2\cdot 0+2\cdot 0=0$$
- $$P(2,0)=2\cdot 2+2\cdot 0=4$$
- $$P(2,1)=2\cdot 2+2\cdot 1=6$$
- $$P(0,2)=2\cdot 0+2\cdot 2=4$$
Vemos que el perímetro se maximiza en el punto $$(2,0)$$. La función perímetro toma allí su valor óptimo, que es $$6$$ metros. Las coordenadas del punto nos están diciendo que maximizará el perímetro haciendo mesas de lado largo ($$x$$) de $$2$$ metros y lado corto ($$y$$) de $$1$$ metro. Ya hemos resuelto el primer problema completo de programación lineal.
Otros ejemplos:
Los $$400$$ alumnos de un colegio van a ir de excursión. Para ello se contrata el viaje a una empresa que dispone de $$8$$ autobuses del tipo A con $$40$$ plazas y $$10$$ del tipo B con $$50$$ plazas, pero sólo de $$9$$ conductores para ese día. Dada la diferente capacidad y calidad, el alquiler de cada autobús de los grandes (tipo B) cuesta $$80$$ € y el de cada uno de los pequeños (tipo A), $$60$$ €. ¿Cuántos autobuses de cada clase convendrá alquilar para que el viaje resulte lo más económico posible?
Primero identificamos las variables. En este caso serán el número de autobuses del tipo A (al que llamaremos $$x$$) y el número de autobuses del tipo B (al que llamaremos $$y$$). La función objetivo es el precio y se ha de minimizar. El precio en función de las variables del problema será la suma de lo que vale un autobús del tipo A (a $$60$$€) multiplicado por el número de autobuses del tipo A que se alquilan más lo mismo, pero de los autobuses tipo B (a $$80$$€). Es decir, el precio será: $$$P(x,y)=60\cdot x+80\cdot y$$$
Las restricciones del problema en forma de inecuaciones:
-
$$x\geqslant 0$$, $$y\geqslant 0$$ (por lógica, no podemos alquilar un número negativo de autobuses).
-
$$x\leqslant 8$$ (sólo hay $$8$$ autobuses del tipo A).
-
$$y\leqslant 10$$ (sólo hay $$10$$ autobuses del tipo B).
-
$$x+y\leqslant 9$$ (sólo hay $$9$$ conductores).
- $$40\cdot x +50\cdot y\geqslant 400$$ (queremos que el número total de plazas de autobús sea disponibles sea como mínimo igual al número de alumnos).
Buscamos las rectas asociadas a las inecuaciones, las zonas de validez de cada inecuación y la zona factible común a todas las restricciones.
Y la zona factible queda:
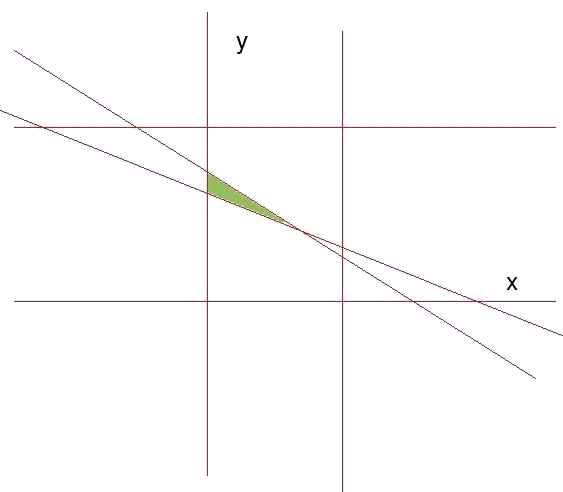
El siguiente paso es calcular los vértices de la región de validez. En este caso son: $$$ (0,8) \qquad (0,9) \qquad (5,4)$$$
La función objetivo (el precio) toma los siguientes valores en los vértices de la región de soluciones factibles:
- $$P(0,8)=60\cdot 0+80\cdot 8=640$$ €
- $$P(0,9)=60\cdot 0+80\cdot 9=720$$ €
- $$P(5,4)=60\cdot 5+80\cdot 4=620$$ €
como queremos minimizar el precio, el punto que queremos es el $$(5,4)$$ y el precio toma el valor de $$620$$ €. Por lo tanto, minimizaremos el precio si se alquilan $$5$$ autobuses del tipo A ($$x$$) y $$4$$ autobuses del tipo B ($$y$$) y todo saldrá por $$620$$ €.
En resumen, en todo problema de programación lineal tendremos que seguir los mismos pasos:
- Elegir las variables del problema.
- Escribir la función objetivo en función de los datos del problema.
- Escribir las restricciones en forma de inecuaciones.
- Determinar la región factible que indican las restricciones.
- Calcular las coordenadas de los vértices de la región de soluciones factibles.
- Calcular el valor de la función objetivo en cada uno de los vértices para ver en cuál de ellos presenta el malor máximo o mínimo, según nos pida el problema.
