Comencem per uns casos particulars:
S'han de transportar $$5$$ cadires d'escriptori que pesen $$10$$ kg cadascuna i $$3$$ taules de $$20$$ kg cadascuna. Es disposa d'un camió que pot transportar $$1000$$ kg de pes. Òbviament, com es compleix que el pes total de cadires més el pes de les taules ($$ 5\cdot10\ \text{kg} +3\cdot20\ \text{kg}= 110\ \text{kg} $$) és menor al pes que pot transportar el camió ($$1000$$ kg), es podrà fer d'una sola vegada. Es pot expressar això matemàticament, afirmant que es compleix la següent desigualtat:
$$$ 5\cdot10\ \text{kg} +3\cdot20\ \text{kg} < 1000\ \text{kg}$$$
Ara s'han de transportar $$20$$ cadires de $$10$$ kg i $$40$$ taules de $$20$$ kg cadascuna. Aquesta vegada hem de mirar si es compleix que el pes total de taules més cadires és inferior o igual al pes que pot transportar el camió:
$$$ 20\cdot10\ \text{kg} + 40\cdot20\ \text{kg} =1000 \ \text{kg}$$$
Així doncs podrem transportar tot d'una sola vegada.
Llavors si es tenen un nombre indeterminat $$x$$ de cadires de $$10$$ kg i un nombre de taules també indeterminat $$y$$, sabrem que la limitació de pes que es pot portar al camió d'una sola vegada és:
$$$x\cdot10\ \text{kg} + y\cdot20\ \text{kg} \leqslant1000 \ \text{kg}$$$
Aquesta última expressió és el que es coneix com una inequació ( $$\leqslant$$ ) lineal de dues variables ($$x$$ i $$y$$). Lineal vol dir que la inequació depèn només d'una combinació lineal de $$x$$ i $$y$$ (és a dir, no apareix cap potència superior de les variables). Es llegeix: el pes de les cadires ($$x\cdot10$$ kg) més el pes de les taules ($$y\cdot20$$ kg) és igual o inferior al pes que pot transportar el camió ($$1000$$ kg).
És interessant determinar quin conjunt de punts $$(x,y)$$ compleixen la inequació. Per saber això, es pot dibuixar la inequació en el pla XY. Cal aïllar $$y$$ a la inequació:
$$$ y\leqslant -\dfrac{10\ \text{kg}}{20\ \text{kg}}\cdot x +\dfrac{1000\ \text{kg}}{20\ \text{kg}}$$$
Prenent estrictament el signe d'igualtat ($$=$$) es té l'equació d'una recta de pendent $$-\dfrac{10\ \text{kg}}{20\ \text{kg}}=-0.5$$ i ordenada en l'origen (és a dir, alçada a la que talla amb l'eix $$y$$) $$\dfrac{1000\ \text{kg}}{20\ \text{kg}}=50$$.
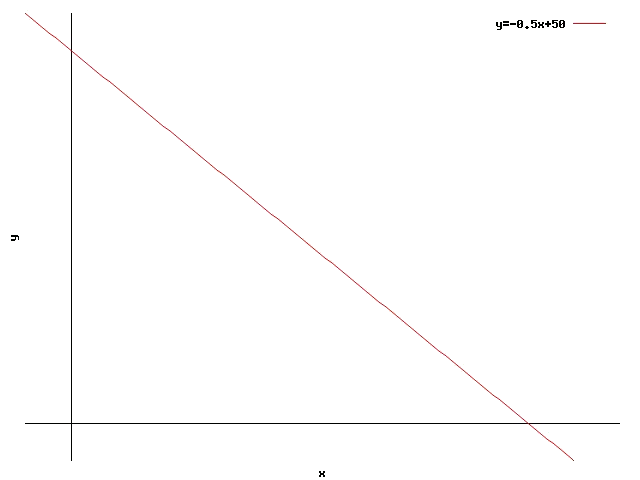
Aquesta recta ens separa els punts en què es compleix la inequació (regió de validesa) dels punts en què no es compleix. Per saber quin costat és cada un s'ha de provar algun dels punts en la inequació, per veure si es compleix o no. Per exemple, es pot provar el punt $$(x=0,y=55)$$. La inequació en aquest punt és:
$$$ 0\cdot10\ \text{kg} + 55\cdot20\ \text{kg} \nleqslant 1000 \ \text{kg} $$$
En aquest punt la inequació no es compleix (el costat de la dreta suma $$1100$$ kg). Per tant els punts per sobre de la recta no compleixen la inequació, mentre que els que estan per sota (o pertànyen a la recta) sí que la compleixen.

Altres exemples:
Les restriccions pesqueres imposades per la CEE obliguen a certa empresa a pescar com a màxim $$3000$$ tones en total de lluç i rap.
Primer s'han d'identificar les variables. Anomenarem $$x$$ a la quantitat de lluç (en tones) i $$y$$ a la quantitat de rap (també en tones). Així doncs aquesta restricció es farà segons la inequació:
$$$ x+ y \leqslant 3000 $$$
La recta associada a aquesta inequació és: $$\ y=-x+3000$$
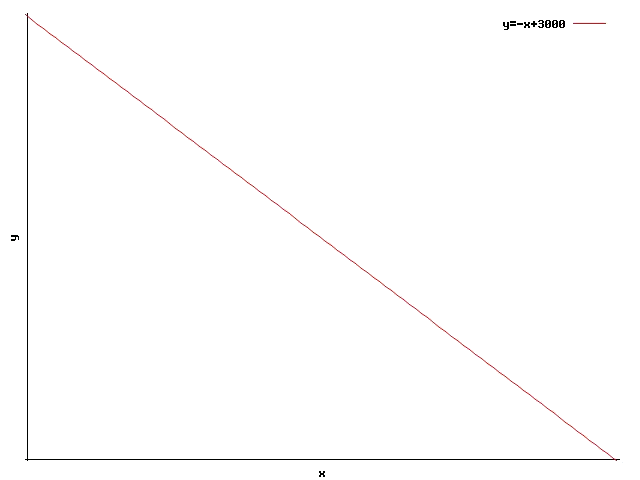
Per saber quina de les meitats del pla és la zona de validesa s'ha de provar un punt. En fer la prova amb el punt $$(x=0,y=0)$$:
$$$ 0+0\leqslant 3000$$$
es compleix la inequació a $$(0,0)$$, per tant la regió de validesa és la que queda per sota de la recta:
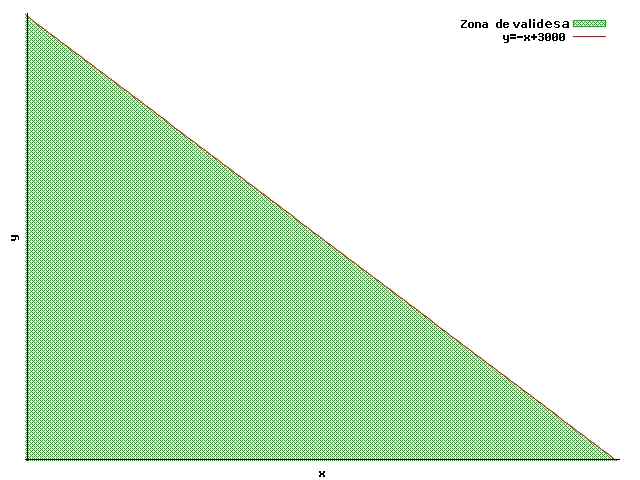
En una fàbrica de pantalons últim model, que porten cremalleres i forats distribuïts per el seu material, es controla que tots els pantalons tinguin com a mínim tres forats.
Com abans, primer s'identifiquen les variables del problema. En aquest cas seran el nombre de cremalleres $$x$$ i el nombre de forats $$y$$. En aquest cas, la restricció serà:
$$$ y\geqslant 3 $$$
Veiem en aquesta inequació dues característiques diferents a les de les inequacions vistes abans. El primer que veiem és que en la restricció només apareix una de les variables, i el segon és que aquesta vegada tenim un signe de major o igual ($$\geqslant$$), En lloc del símbol de menor o igual ($$\leqslant$$). Tot i així aquesta inequació té les mateixes propietats que les vistes abans. Es pot veure que la recta associada a aquesta inequació és una constant: $$y=3$$
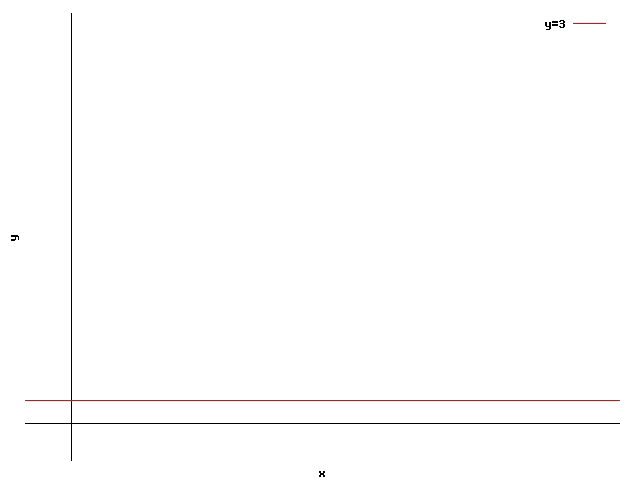
Per saber quina de les dues és la regió de validesa, provem la inequació amb el punt $$(x=0,y=0)$$: $$$ 0\ngeqslant 3 $$$
$$(0,0)$$ no compleix la inequació, per tant la regió de validesa és el semiplà superior.
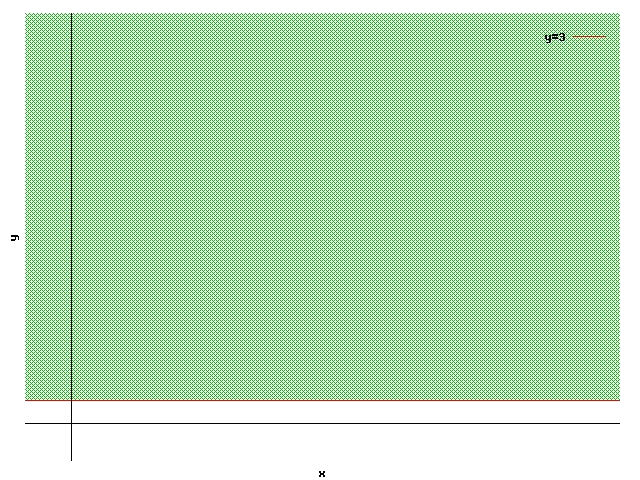
Això era obvi només veient la inequació: $$y\geqslant 3$$.
Un repartidor pot repartir tants paquets com pugui, mentre que no s'excedeixi de $$200$$ km al dia.
De nou primer identifiquem les variables. Anomenarem $$x$$ al nombre de quilòmetres que fa i $$y$$ al nombre de paquets que reparteix. En aquest cas la restricció serà la següent inequació:
$$$ x\leqslant 200 $$$
En aquest cas també depèn només d'una de les variables. No podem aïllar la $$y$$, perquè no apareix, però ja sabem que aquesta restricció es representarà per una recta vertical (paral·lela a l'eix $$y$$) que separi els valors de $$x$$ superiors i inferiors a $$200$$, i ens quedarem amb la zona de $$x$$ menor o igual a $$200$$:

Un pastisser té $$150$$ kg de farina per fer dos tipus de pastissos P i Q. Per fer una dotzena de pastissos de tipus P necessita $$3$$ kg de farina i per fer una dotzena de tipus Q necessita 6 kg de farina.
S'identifiquen primer les variables. En aquest cas seran el nombre de pastissos del tipus P ($$x$$) i el nombre de pastissos del tipus Q ($$y$$). Per fer un pastís de tipus P es necessiten $$\dfrac{3}{12} \text{kg}= \dfrac{1}{4} \text{kg}$$ de farina (els $$3$$ kg que es necessiten per fer $$12$$ pastissos, dividit per aquests $$12$$ pastissos). Per un del tipus Q es necessiten $$\dfrac{6}{12} \text{kg}= \dfrac{1}{2} \text{kg}$$ de farina. Així doncs, la restricció serà que la farina que s'usi no pot superar els $$150$$ kg de què disposa el pastisser:
$$$ \dfrac{1}{4} \cdot x+\dfrac{1}{2}\cdot y\leqslant 150 $$$
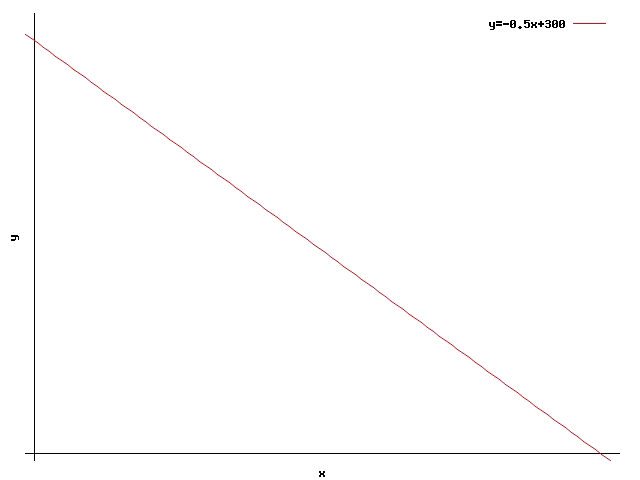
La recta associada a aquesta inequació és: $$y=-\dfrac{1}{2}\cdot x+300$$
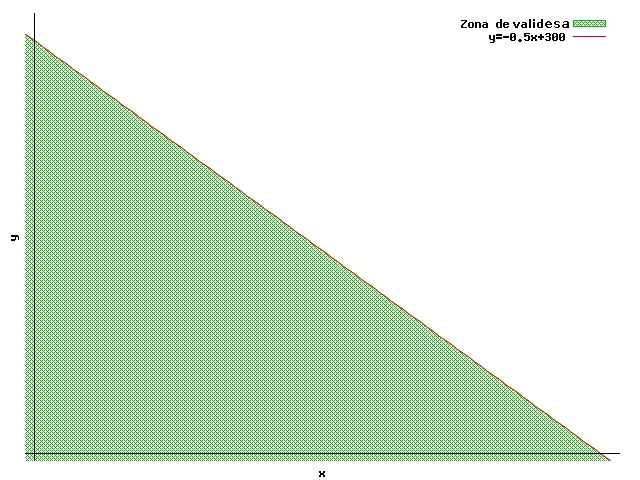
Ara es comprova si el punt $$(x=0,y=0)$$ compleix la inequació o no, per esbrinar quin dels dos semiplans és la regió de validesa:
$$$ \dfrac{1}{4} \cdot 0+\dfrac{1}{2}\cdot 0\leqslant 150 $$$
Es compleix la inequació al punt $$(0,0)$$, per tant la regió de validesa és la que queda per sota de la recta:
En resum:
Quan tinguem una restricció, aquesta es podrà escriure com una inequació. Primer s'han d'identificar les variables i s'ha d'escriure la inequació: $$$ a\cdot x+ b \cdot y \leqslant c$$$
La recta associada serà: $$\ y=-\dfrac{a}{b} \cdot x+\dfrac{c}{b}$$
(Excepte en el cas en què $$b=0$$. En aquest cas no apareix la variable $$y$$ a la inequació i la recta associada és paral.lela a l'eix $$y$$, separant els valors de $$x$$ entre els que compleixen la inequació i els que no).
Finalment s'hauria de mirar quin dels semiplans en què separa la recta al pla és la zona en què es compleix la inequació (regió de validesa). El més fàcil és mirar si el punt $$(x=0,y=0)$$ compleix la inequació o no. Si $$(0,0)$$ compleix la inequació, la zona a la qual pertany és la regió de validesa. En cas contrari serà l'altra zona la regió de validesa.
