Comencemos por unos casos particulares:
Se tienen que transportar $$5$$ sillas de escritorio que pesan $$10$$ kg cada una y $$3$$ mesas de $$20$$ kg cada una. Se dispone de un camión que puede transportar $$1000$$ kg de peso. Obviamente, como se cumple que el peso total de sillas más el peso de las mesas ($$ 5\cdot10\ \text{kg} +3\cdot20\ \text{kg}= 110\ \text{kg} $$) es menor al peso que puede transportar el camión ($$1000$$ kg), se podrá hacer de una sola vez. Se puede expresar esto matemáticamente, afirmando que se cumple la siguiente desigualdad:
$$$ 5\cdot10\ \text{kg} +3\cdot20\ \text{kg} < 1000\ \text{kg}$$$
Ahora se tienen que transportar $$20$$ sillas de $$10$$ kg y $$40$$ mesas de $$20$$ kg cada una. Esta vez hemos de mirar si se cumple que el peso total de mesas más sillas es inferior o igual al peso que puede transportar el camión:
$$$ 20\cdot10\ \text{kg} + 40\cdot20\ \text{kg} =1000 \ \text{kg}$$$
Así pues podremos transportar todo de una sola vez.
Entonces si se tienen un número indeterminado $$x$$ de sillas de $$10$$ kg y un número de mesas también indeterminado $$y$$, sabremos que la limitación de peso que se puede llevar en el camión de una sola vez es:
$$$x\cdot10\ \text{kg} + y\cdot20\ \text{kg} \leqslant1000 \ \text{kg}$$$
Esta última expresión es lo que se conoce como una inecuación ( $$\leqslant$$) lineal de dos variables ($$x$$ e $$y$$). Lineal quiere decir que la inecuación depende sólo de una combinación lineal de $$x$$ e $$y$$ (no aparece ninguna potencia superior de las variables). Se lee: el peso de las sillas ($$x\cdot10$$ kg) más el peso de las mesas ($$y\cdot20$$ kg) es igual o inferior al peso que puede transportar el camión ($$1000$$ kg).
Es interesante determinar qué conjunto de puntos $$(x,y)$$ cumplen la inecuación. Para saber esto,se puede dibujar la inecuación en el plano XY. Es necesario despejar $$y$$ en la inecuación:
$$$ y\leqslant -\dfrac{10\ \text{kg}}{20\ \text{kg}}\cdot x +\dfrac{1000\ \text{kg}}{20\ \text{kg}}$$$
Tomando estrictamente el signo de igualdad ($$=$$) se tiene la ecuación de una recta de pendiente $$-\dfrac{10\ \text{kg}}{20\ \text{kg}}=-0.5$$ y ordenada en el origen (es decir, altura a la que corta con el eje $$y$$) $$\dfrac{1000\ \text{kg}}{20\ \text{kg}}=50$$.
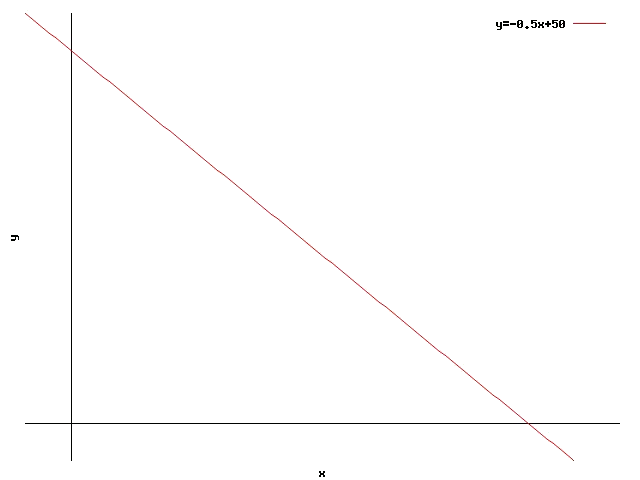
Esta recta nos separa los puntos en que se cumple la inecuación ( región de validez ) de los puntos en que no se cumple.Para saber qué lado es cada cual se ha de probar alguno de los puntos en la inecuación, para ver si se cumple o no. Por ejemplo, se puede probar el punto $$(x=0,y=55)$$. La inecuación en este punto es:
$$$ 0\cdot10\ \text{kg} + 55\cdot20\ \text{kg} \nleqslant 1000 \ \text{kg} $$$
En este punto la inecuación no se cumple (el lado de la derecha suma $$1100$$ kg). Por lo tanto los puntos por encima de la recta no cumplen la inecuación, mientras que los que están por debajo (o sobre la recta) sí que la cumplen.
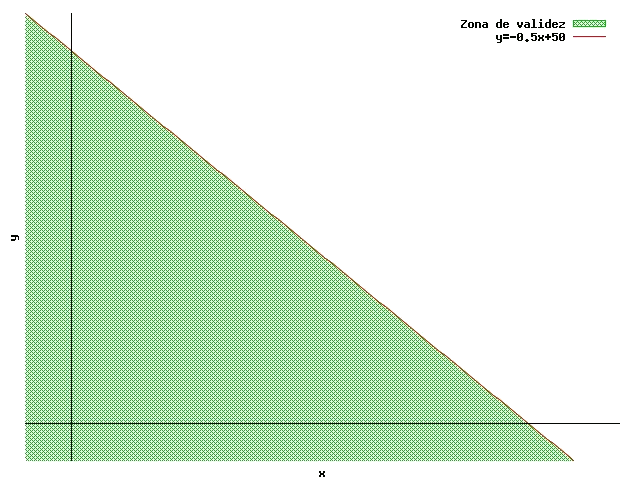
Otros ejemplos:
Las restricciones pesqueras impuestas por la CEE obligan a cierta empresa a pescar como máximo $$3000$$ toneladas en total de merluza y rape.
Primero se han de identificar las variables. Llamaremos $$x$$ a la cantidad de merluza pescada (en toneladas) e $$y$$ a la cantidad de rape pescado (también en toneladas). Así pues esta restricción vendrá dada por la inecuación:
$$$ x+y\leqslant 3000 $$$
La recta asociada a esta inecuación es: $$\ y=-x+3000$$
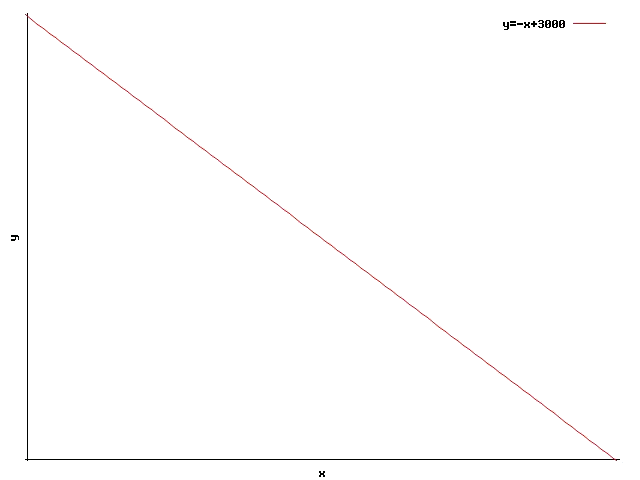
Para saber cual de las mitades del plano es la zona de validez se ha de probar un punto. Al hacer la prueba con el punto $$(x=0,y=0)$$:
$$$ 0+0\leqslant 3000$$$
se cumple la inecuación en $$(0,0)$$, por lo tanto la región de validez es la que queda por debajo de la recta:
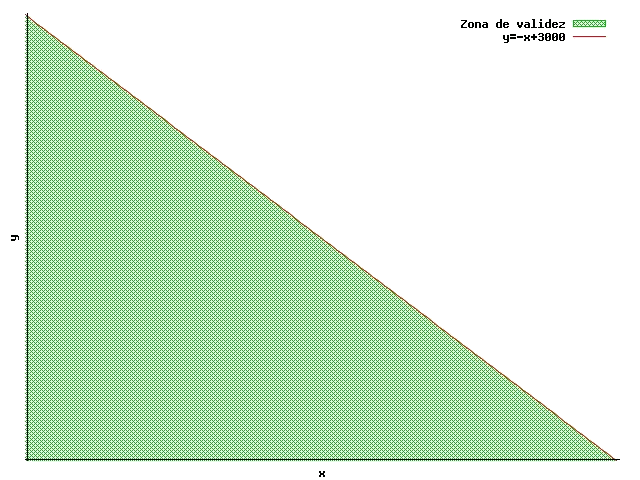
En una fábrica de pantalones último modelo, que llevan cremalleras y agujeros distribuidos por su material, se controla que todos los pantalones tengan como mínimo tres agujeros.
Como antes, primero se identifican las variables del problema. En este caso serán el número de cremalleras $$x$$ y el número de agujeros $$y$$. En este caso, la restricción será:
$$$ y\geqslant 3 $$$
Vemos en esta inecuación dos características distintas a las de las inecuaciones vistas antes. Lo primero que vemos es que en la restricción solo aparece una de las variables, y lo segundo es que esta vez tenemos un signo de mayor o igual ($$\geqslant$$), en lugar del símbolo de menor o igual ($$\leqslant$$). Aún y así esta inecuación tiene las mismas propiedades que las vistas antes. Se puede ver que la recta asociada a esta inecuación es una constante: $$y=3$$
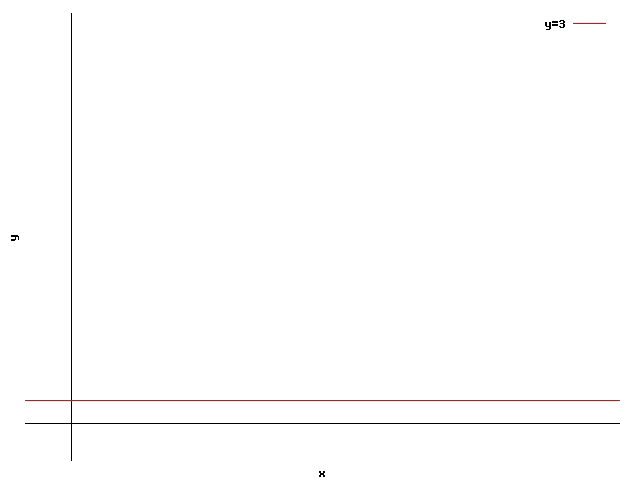
Para saber cual de las 2 es la región de validez, probamos la inecuación con el punto $$(x=0,y=0)$$: $$$ 0\ngeqslant 3 $$$
$$(0,0)$$ no cumple la inecuación, por lo tanto la región de validez es el semiplano superior.
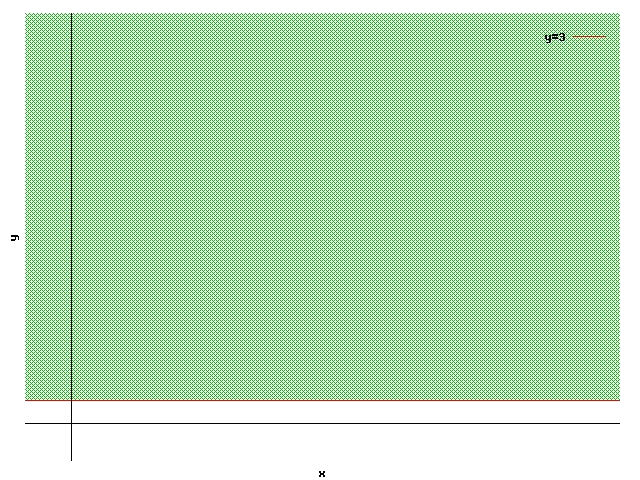
Esto era obvio sólo viendo la inecuación: $$y\geqslant 3$$.
Un repartidor puede repartir tantos paquetes como pueda, mientras que no se exceda de $$200$$ km al día.
De nuevo primero identificamos las variables. Llamaremos $$x$$ al número de kilómetros que hace e $$y$$ al número de paquetes que reparte. En este caso la restricción será la siguiente inecuación:
$$$ x\leqslant 200 $$$
En este caso también depende solo de una de las variables. No podemos despejar la $$y$$, porque no aparece, pero ya sabemos que esta restricción se representará por una recta vertical (paralela al eje $$y$$) que separe los valores de $$x$$ superiores e inferiores a $$200$$, y nos quedaremos con la zona de $$x$$ menor o igual a $$200$$:

Un pastelero tiene $$150$$ kg de harina para hacer dos tipos de pasteles P y Q. Para hacer una docena de pasteles de tipo P necesita $$3$$ kg de harina y para hacer una docena de tipo Q necesita 6 kg de harina.
Se identifican primero las variables. En este caso serán el número de pasteles del tipo P ($$x$$) y el número de pasteles del tipo Q ($$y$$). Para hacer un pastel del tipo P se necesitan $$\dfrac{3}{12} \text{kg}= \dfrac{1}{4} \text{kg}$$ de harina (los $$3$$ kg que se necesitan para hacer $$12$$ pasteles, dividido por esos $$12$$ pasteles). Para uno del tipo Q se necesitan $$\dfrac{6}{12} \text{kg}= \dfrac{1}{2} \text{kg}$$ de harina. Así pues, la restricción será que la harina que se use no puede superar los $$150$$ kg de que dispone el pastelero:
$$$ \dfrac{1}{4} \cdot x+\dfrac{1}{2}\cdot y\leqslant 150 $$$
La recta asociada a esta inecuación es: $$y=-\dfrac{1}{2}\cdot x+300$$
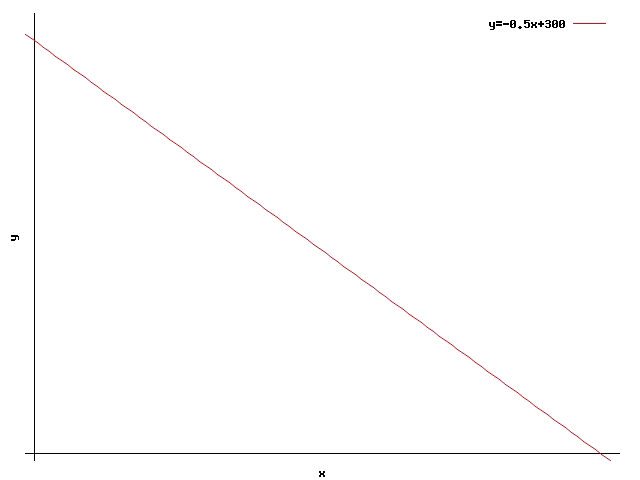
Ahora se comprueba si el punto $$(x=0,y=0)$$ cumple la inecuación o no, para averiguar cuál de los dos semiplanos es la región de validez:
$$$ \dfrac{1}{4} \cdot 0+\dfrac{1}{2}\cdot 0\leqslant 150 $$$
Se cumple la inecuación en el punto $$(0,0)$$, por lo tanto la región de validez es la que queda por debajo de la recta:
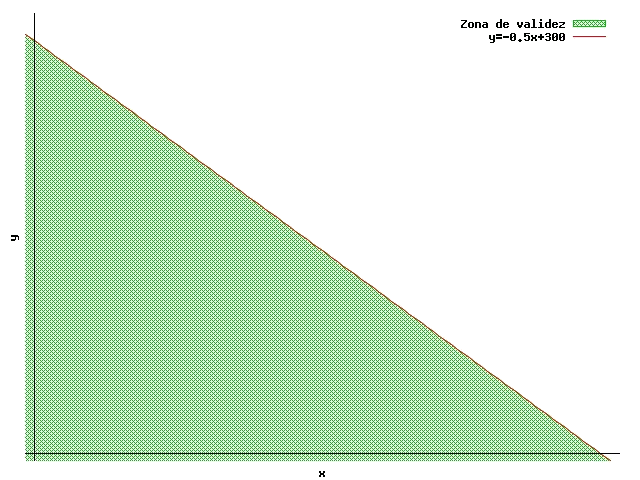
En resumen:
Cuando se tenga una restricción, ésta se podrá escribir como una inecuación. Primero se han de identificar las variables y se ha de escribir la inecuación: $$$ a\cdot x+ b \cdot y \leqslant c$$$
La recta asociada será: $$\ y=-\dfrac{a}{b} \cdot x+\dfrac{c}{b}$$
(Excepto en el caso en que $$b=0$$. En ese caso no aparece la variable $$y$$ en la inecuación y la recta asociada es paralela al eje $$y$$, separando los valores de $$x$$ entre los que cumplen la inecuación y los que no).
Por último se tendría que mirar cual de los semiplanos en que separa la recta al plano es la zona en que se cumple la inecuación (región de validez). Lo más fácil es mirar si el punto $$(x=0,y=0)$$ cumple la inecuación o no. Si $$(0,0)$$ cumple la inecuación, la zona a la que pertenece es la región de validez. En caso contrario será la otra zona la región de validez.
