Concavitat i convexitat
Es diu que una funció $$f(x)$$ és convexa si en unir dos punts qualssevol de la gràfica, el segment traçat queda per sobre de la gràfica:
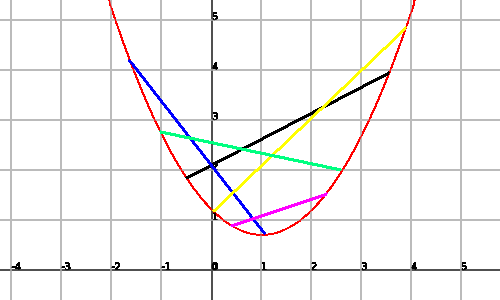
En aquesta imatge podem observar amb diferents colors diferents segments que uneixen dos punts de la gràfica i que queden per sobre d'ella.
Un exemple de funció no convexa és:
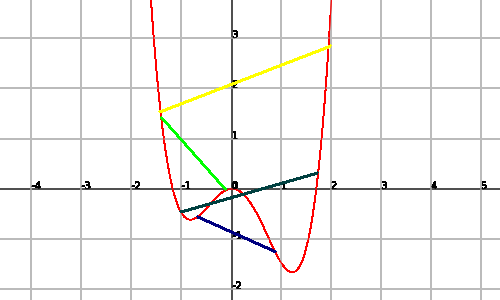ja que trobem segments que uneixen dos punts de la gràfica i que passen per sota d'aquesta.
D'altra banda, es diu que una funció $$f(x)$$ és còncava si la funció $$-f(x)$$ és convexa, és a dir, si els segments que uneixen els punts de la gràfica de $$f(x)$$ estan tots situats per sota de la gràfica.
Vegem un exemple de funció còncava:
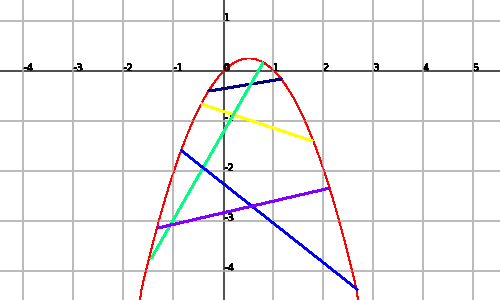
Vulgarment, podem dir que les funcions convexes són funcions corbes que presenten primer un descens i després un ascens i les funcions còncaves funciona al revés, primer un ascens i després un descens.
Les funcions, però, poden presentar parts còncaves i parts convexes en una mateixa gràfica, per exemple, la funció $$f(x)=(x+1)^3-3(x+1)^2+2$$ presenta concavitat en l'interval $$(-\infty,0)$$ i convexitat en l'interval $$(0,\infty)$$:
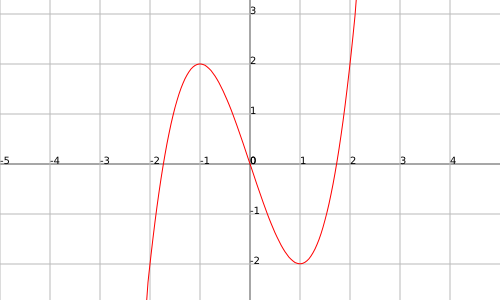
L'estudi de la concavitat i convexitat es realitza a través dels punts d'inflexió.
Punts d'inflexió
Es defineix un punt d'inflexió com el punt en què la funció passa de ser convexa a còncava o de còncava a convexa.
Podem veure en l'exemple anterior que en el punt $$x=0$$ (en l'origen de coordenades) la funció passa de ser còncava a ser convexa, per tant diem que $$x=0$$ és punt d'inflexió.
Una característica dels punts d'inflexió és que són els punts on la funció derivada té màxims i mínims. Si ens fixem, quan ens acostem a un punt d'inflexió la funció cada vegada creix més (o decreix menys), però al sobrepassar el punt d'inflexió la funció comença a créixer menys (o decréixer menys). Això vol dir que justament on hi hagi un punt d'inflexió la derivada tindrà un màxim o un mínim. Conseqüentment trobarem els punts d'inflexió buscant zeros de la segona derivada.
Anem a il·lustrar el procés amb un exemple per així donar una explicació simple i clara:
Considerarem la funció $$f(x)=x^3-3x$$ (és la funció representada en l'anterior gràfica).
Sabem ja calcular els màxims i els mínims de la funció $$f(x)$$ usant la primera derivada. L'expressió d'aquesta és $$f'(x)=3x^2-3$$ i trobem un màxim i un mínim respectivament en $$x=-14$$ i $$x=1$$. Si representem la gràfica de la derivada tenim:
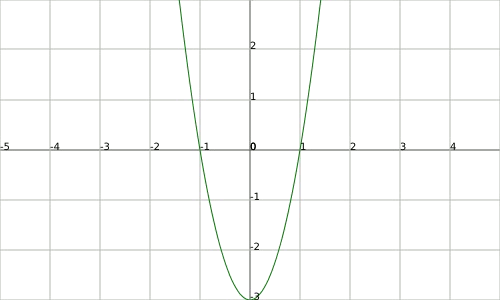
Observem que justament on la derivada té un mínim és on la funció té el punt d'inflexió.
Per trobar el punt anem a derivar la funció derivada i igualar a zero: $$$f''(x)=6x \Rightarrow 6x=0 \Rightarrow x=0$$$ i per tant la funció original en $$x=0$$ té un punt d'inflexió.
El procés per trobar els punts d'inflexió, igual que els màxims i mínims, és un procés algorítmic i molt mecànic. Derivar la funció dues vegades, igualar a zero i trobar les solucions de l'equació. Aquestes solucions justament seran on tinguem punts d'inflexió.