La recta tangent a una corba és la que coincideix amb la corba en un punt i amb la mateixa derivada, és a dir, el mateix grau de variació.
El coneixement de la recta tangent permetrà resoldre problemes senzills: en primer lloc, es podran trobar tangents a qualsevol funció que es pugui derivar, en qualsevol punt, com s'observa en el primer exemple resolt a continuació. En segon lloc i com es pot veure en el segon exemple, es pot utilitzar com a condició en problemes més complexos.
La recta $$y= m\cdot x +b$$ és tangent a la corba $$f(x)$$ si compleix els següents requisits:
- Passa pel punt de tangència: $$(a,f(a))$$
- Té el mateix pendent (mateix valor de la derivada) que la corba en el punt de tangència: $$m=f'(a)$$
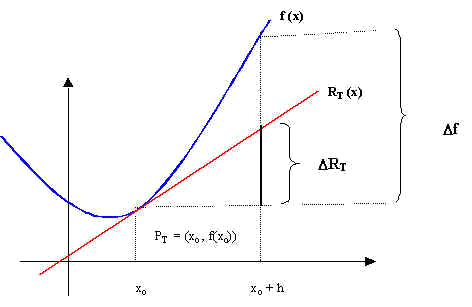
Llavors, es pot escriure l'equació de la recta tangent de la següent manera:$$$y-f(a)=f'(a)\cdot (x-a)$$$
Nota: Sempre es trobaran tangents a funcions polinòmiques d'ordre superior a 1, o funcions no polinòmiques. La tangent a una recta seria la mateixa recta.
A més, la recta tangent pot tenir interessants aplicacions geomètriques. La següent gràfica posició-temps mostra l'evolució d'un atleta des de que comença a córrer. Es pot veure que l'eix vertical representa la distància recorreguda, mentre que l'horitzontal representa el temps en segons.
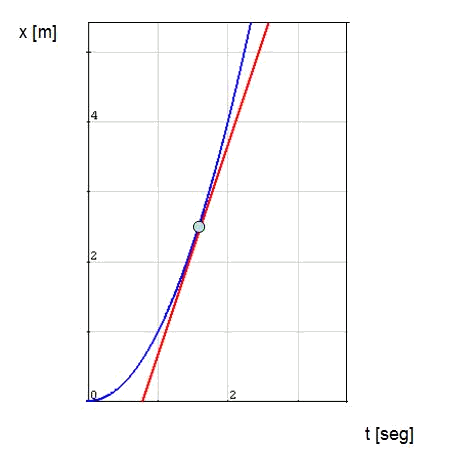
Tenint en compte que la velocitat és la derivada de la posició respecte al temps, el pendent de la paràbola blava representa la velocitat instantània.
Es pot veure que el corredor comença amb velocitat nul·la (parat) i va accelerant. La recta vermella de la gràfica representa un altre corredor que va a una velocitat constant i, en l'instant marcat pel punt de tangència, té la mateixa velocitat i es troba al mateix punt. El segon corredor va més ràpid que el primer fins que és avançat, i després és el primer el que, gràcies a que està accelerant, acaba per davant.
Vegem alguns exemples:
Troba la recta tangent a $$f(x)=\sin x$$ en $$x=\pi$$.
a) Es busquen les coordenades del punt de tangència $$P$$: $$$\begin{array}{l} f(\pi)=0 \\ P=(\pi,0) \end{array}$$$
b) Es troba la derivada de $$f(x)$$ en $$x=\pi$$: $$$\begin{array}{l} f'(x)=\cos x \\ f'(\pi)= -1 \end{array}$$$
Tenim ja el pendent de la recta tangent.
Llavors, s'escriu: $$$\begin{array} {l} y-0=-1 \cdot (x -\pi) \\ y= \pi-x\end{array}$$$
Trobar l'equació de la recta tangent a la paràbola $$f(x)=x^2-5x+6$$ i paral·lela a la recta $$3x+y-2=0$$
a) S'escriu la recta de la manera següent: $$$y=-3s+2$$$ Atès que la tangent que es vol trobar serà paral·lela a aquesta recta, tindrà una pendent $$m=-3$$
b) Només falta trobar el punt de tangència $$(a,f(a))$$, és a dir, el punt en què la paràbola tindrà una derivada de valor $$m$$: $$$f'(x)=2x-5$$$ I en el punt $$a$$, $$$\begin{array} {l} f'(a)=2a-5=-3 \\ a=1 \\ f(a)=2 \end{array}$$$ Finalment, l'equació de la recta tangent serà: $$$\begin{array}{l}y-2=-3 \cdot (x-1) \\ y=-3x+5 \end{array}$$$
