Tangent straight line to a curve at a point

The tangent straight line to a curve is the line that touches the curve only at a point and has a slope equal to the derivative at that point.

Knowing the tangent straight line will allow us to solve simple problems: First, we will be able to find the tangent to any function that we want, at any point, as we will see in the following example. Second, as we will see in the second example, we will be able to use the tangent for more complex problems.

The straight line $$y= m\cdot x +b$$ is tangent to the curve $$f(x)$$ if it satisfies the following conditions:

1. It touches the point: $$(a,f(a))$$
2. It has the same slope than the derivative of the curved line at the touching point: $$m=f'(a)$$

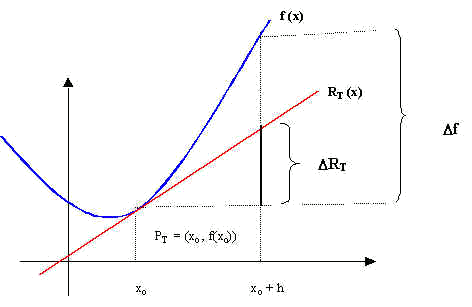
If these two points are satisfied, then it is possible to express the tangent line as follows:$$$y-f(a)=f'(a)\cdot (x-a)$$$

Note: We can always find tangent lines to polynomials of order greater than 1 and to any none polynomic function. Note, however, that the tangent to a straight line is the straight line itself.

Also, the tangent straight line can have interesting geometric applications. The following figure showing position - time shows the evolution of an athlete from the moment he starts running. We have that the vertical axis represents the covered distance, while the horizontal one represents the time in seconds.

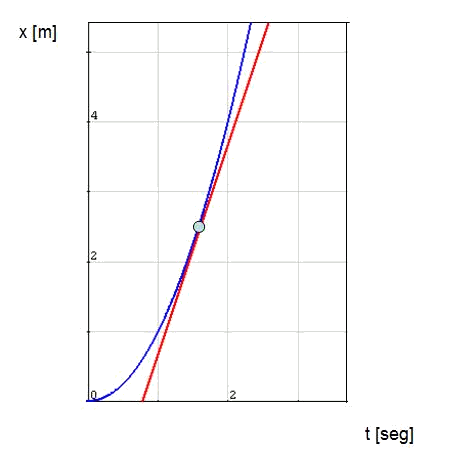
Bearing in mind that the speed is the derivative of the position with regard to the time, the slope of the blue parable represents the instantaneous speed.

It is possible to see that the runner starts with zero speed (stopped) and he accelerates. The red straight line of the graph represents another runner that goes at a constant speed and, in the moment when the two lines touch each other, it has the same speed and it is at the same point.

First the second runner runs faster until the point he reaches the first runner. At this point the second runner runs more and keeps accelerating.

Let's see some examples: