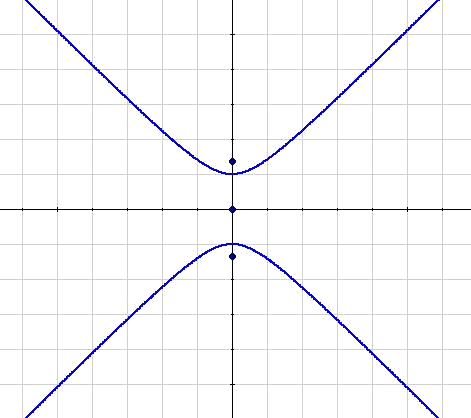
Tractarem ara les hipèrboles reduïdes verticals. En aquest cas, és l'eix d'ordenades el que correspon amb l'eix focal.
El lloc geomètric dels focus és llavors $$F'(0,-c)$$ i $$F(0,c)$$. Aplicant ara la definició general obtenim $$$\displaystyle \sqrt{x^2+(y+c)^2}-\sqrt{x^2+(y-c)^2}=2a$$$
Passem a l'altre membre l'arrel que està restant, i elevem al quadrat: $$$\displaystyle \begin{array} {rcl} \Big(\sqrt{x^2+(y+c)^2}\Big)^2 & = & \Big(2a+\sqrt{x^2+(y-c)^2}\Big)^2 \\ x^2+(y+c)^2 & = & 4a^2+4a\sqrt{x^2+(y-c)^2}+x^2+(y-c)^2 \\ x^2+y^2+2yc+c^2 & = & 4a^2+4a \sqrt{x^2+(y-c)^2}+x^2+y^2-2yc+c^2 \end{array} $$$
Al simplificar i dividint per quatre: $$$\displaystyle \begin{array} {rcl} 4yc & = & 4a^2+4a\sqrt{x^2+(y-c)^2} \\ yc & = & a^2+a\sqrt{x^2+(y-c)^2} \end{array} $$$
En aïllar l'arrel i elevar novament al quadrat: $$$\begin{array}{rcl} (cy-a^2)^2 & = & \Big(a+ \sqrt{x^2+(y-c)^2}\Big)^2 \\ c^2y^2-2a^2cy+a^4 & = & a^2(x^2+(y-c)^2)\\ c^2y^2-2a^2cy+a^4 & = &a^2(x^2+y^2-2cy+c^2) \\c^2y^2-a^2y^2- a^2x^2& = &a^2c^2-a^4 \\(c^2-a^2)y^2-a^2x^2 & = & a^2(c^2-a^2)\end{array}$$$
Dividir llavors entre $$a^2(c^2-a^2)$$ per obtenir un $$1$$ a la dreta: $$$\displaystyle\begin{array}{rcl} \frac{(c^2-a^2)y^2}{a^2(c^2-a^2)}-\frac{a^2x^2}{a^2(c^2-a^2)}&=&1 \\ \frac{y^2}{a^2}-\frac{x^2}{(c^2-a^2)} & = & 1\end{array}$$$
En aplicar la definició $$c^2=a^2+b^2$$, $$b^2=c^2-a^2$$ es substitueix i s'arriba a l'equació desitjada per a la hipèrbola reduïda vertical: $$$\displaystyle \frac{y^2}{a^2}-\frac{x^2}{b^2}=1$$$
