S'anomena circumferència al lloc geomètric dels punts del pla que equidisten d'un punt fix anomenat centre. A la distància se l'anomena radi.
Aquesta propietat és la clau per trobar l'expressió analítica d'una circumferència.
Vegem com:
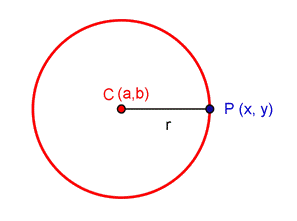
Una circumferència de centre $$C = ( a, b)$$ i radi $$r$$, està formada per tots els punts $$P = (x, y)$$ la distància al centre és $$r$$.
Expressant això en forma d'equació matemàtica tenim: $$$\displaystyle d(C,P)=d((a,b),(x,y))= \sqrt{(x-a)^2+(y-b)^2} =r$$$ Elevant al quadrat aquesta equació obtenim l'equació reduïda de la circumferència: $$$ \displaystyle d(C,P)^2=\Big( \sqrt{(x-a)^2+(y-b)^2} \Big)^2=(x-a)^2+(y-b)^2=r^2$$$ Pel que qualsevol expressió del tipus $$$(x-a)^2+(y-b)^2=r^2$$$ és una circumferència de radi $$r$$ i centre el punt $$(a, b)$$.
$$ (x-1)^2+(y-2)^2=3^2$$ és una circumferència de radi $$3$$ i centrada en el punt $$(1, 2)$$.
Quan considerem una circumferència centrada en l'origen, estem agafant $$C = (0, 0)$$ i per tant l'equació és $$x^2+y^2=r^2$$.
$$x^2+y^2=4^2$$ stà centrada en l'origen i té radi $$4$$.
La circumferència amb centre en l'origen i radi 1 s'anomena circumferència unitat.
Si per exemple volem escriure l'equació d'una circumferència centrada en el punt $$(-8, 0)$$ i amb diàmetre $$36$$, el procediment és:
Calculem el radi: $$$\displaystyle r=\frac{\mbox{diameter}}{2}=\frac{36}{2}=18$$$
Substituïm els paràmetres en l'equació de la circumferència, amb $$r=18$$ i $$C = (-8, 0)$$: $$$\displaystyle (x-(-8)^2)+(y-0)^2=18^2 \Rightarrow (x+8)^2+y^2=18^2$$$ I ja tenim l'equació.
