Les funcions que no són contínues poden presentar diferents tipus de discontinuïtats.
Per començar definirem funció discontínua com aquella que no compleix la definició de continuïtat. És a dir, si trobem un punt de discontinuïtat direm que la funció no és contínua:
$$f(x)$$ no és contínua si existeix $$x=a$$ pertanyent al $$Dom(f)$$ tal que $$\displaystyle \lim_{x \to a^{ \pm}}f(x) \neq f(a)$$
Vegem un exemple de funció no contínua:
Prenguem la funció $$f(x)=\left\{ \begin{array}{rcl} 1 & \mbox{ si } & x\leq 0 \\ 2 & \mbox{ si } & x>0 \end{array} \right.$$.
Aquesta funció no és contínua ja que en el punt $$x=0$$ observem que: $$$ \displaystyle \lim_{x \to 0^+} f(x)=\lim_{x \to 0} 2=2 \\ f(0)=1$$$ i com el límit lateral per la dreta no coincideix amb el valor de la funció, deduïm que la funció no pot ser contínua. Podem veure la representació gràfica a continuació:
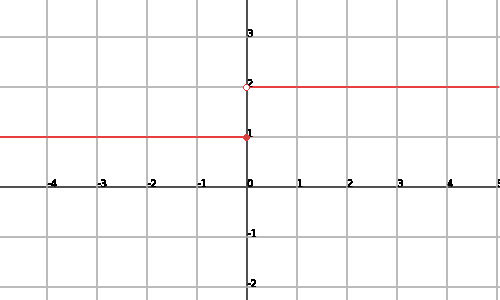
S'ha de tenir en compte que es defineix una discontinuïtat sobre punts del domini d'una funció. Si la funció no està definida en un punt, encara que tingui comportament semblant al d'una discontinuïtat, no en tindria cap, ja que no es podria aplicar la definició de discontinuïtat.
Discontinuïtat evitable
Una discontinuïtat evitable en un punt $$x=a$$ és aquella en què els límits laterals coincideixen, però el valor de la funció en el punt, no, és a dir: $$$\displaystyle \lim_{x \to a^-}f(x)=\lim_{x \to a^+}=L \\ f(a) \neq L$$$ És raonable que anomenem discontinuïtat evitable a aquest tipus de discontinuïtats ja que la funció en el punt de discontinuïtat sembla que sigui contínua, però el punt en concret no existeix, així que només afegint aquest punt, aconseguiríem que la funció fóra contínua (es podria evitar la discontinuïtat molt fàcilment).
Vegem un exemple:
Prenguem la funció $$$\displaystyle \left \{\begin{array}{rcl} \frac{x^2-4}{x+2} & \mbox{ si } & x\neq -2 \\ 0 & \mbox{ si } & x=-2 \end{array} \right.$$$
Podem veure ràpidament que en el punt $$x =-2$$ pot ser que la funció no connecti correctament. Observem doncs la continuïtat en aquest punt: $$$ \displaystyle \begin{array}{l} \lim_{x \to -2^-}f(x)=\lim_{x \to -2^-} \frac{x^2-4}{x+2}=\lim_{x \to -2^-}\frac{(x+2)(x-2)}{x+2}=\lim_{x \to -2^-}x-2=-4 \\ \lim_{x \to -2^+}f(x)=\lim_{x \to -2^+} \frac{x^2-4}{x+2}=\lim_{x \to -2^+}\frac{(x+2)(x-2)}{x+2}=\lim_{x \to -2^+}x-2=-4 \\ f(-2)=0\end{array}$$$
Per tant, $$f (x)$$ té una discontinuïtat evitable en el punt $$x =-2$$.
Prenguem la funció $$$\displaystyle f(x)=\left\{ \begin{array} {rcl} e^x & \mbox{ si } & x < 0 \\ 0 & \mbox{ si } & x=0 \\ x+1 & \mbox{ si } & x>0 \end{array} \right.$$$
Observem ràpidament que les subfuncions que defineixen la nostra funció són contínues. Pel que la funció serà contínua si les seves subfuncions connecten correctament. Pot ser que tinguem problemes en el punt $$x=0$$.
Veiem què passa exactament: $$$\begin{array}{l} \lim_{x \to 0^-} f(x) = \lim_{x \to 0^-}e^x=e^0=1 \\ \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}x+1 =0+1=1 \\ f(0)=0 \end{array}$$$
Per tant, $$f (x)$$ té una discontinuïtat evitable en el punt $$x=0$$.
Discontinuïtat inevitable (o de salt finit)
Una funció $$f(x)$$ té una discontinuïtat inevitable al punt $$x=a$$ si els límits laterals de la funció en aquest punt no coincideixen (i són finits), és a dir: $$$\displaystyle \begin{array} {l} \lim_{x \to a^-}f(x) \neq \lim_{x \to a^+}f(x) \\ f(a)=L \end{array}$$$ independentment del valor de la funció a $$x=a$$ (del valor de $$f(a)$$).
Si ens fixem amb el nom de "inevitable", és raonable que es digui així ja que a diferència de les discontinuïtats evitables, aquesta vegada en no ser iguals els límits laterals no hi ha manera de poder connectar les dues branques de la funció. Amb un exemple veurem clarament el que està passant:
Prenguem la funció $$$f(x)=\left \{ \begin{array}{rcl} x+1 & \mbox{ si } & x \leq 0 \\ x-1 &\mbox{ si } & x>0 \end{array}\right.$$$
podem veure que en el zero tenim: $$$\displaystyle \begin{array}{l} \lim_{x \to 0^-}f(x)=\lim_{x \to 0} x+1=1 \\ \lim_{x \to 0^+}f(x)=\lim_{x \to 0}x-1=-1 \\ f(0)=1\end{array}$$$ i en no coincidir els límits, tenim una discontinuïtat inevitable (tenint fins i tot que $$f (0) =1$$, que significa que tenim continuïtat lateral per l'esquerra).
Podem veure la representació gràfica de la funció:
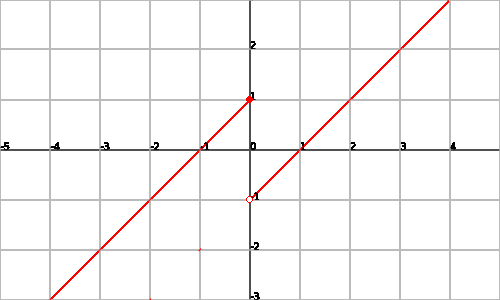
Prenguem la funció $$$f(x)=\left \{ \begin{array}{rcl} e^x & \mbox{ si } & x < 1 \\ x^2 & \mbox{ si } & x \geq 1 \end{array}\right.$$$
La funció serà contínua si en el punt $$x=1$$ els límits laterals i la funció coincideixen. Vegem el seu comportament: $$$ \displaystyle \begin{array} {l} \lim_{x \to 1^-}f(x)=\lim_{x \to 1^-}e^x=e \\ \lim_{x \to 1^+}f(x)=\lim_{x \to 1^+}x^2= 1 \\ f(1)=(1)^2=1 \end{array} $$$
Per tant, tenim una discontinuïtat inevitable.
Discontinuïtat essencial
Una funció $$f(x)$$ té una discontinuïtat essencial en el punt $$x=a$$ si es compleixen algun dels següents casos:
- Els límits laterals no coincideixen.
- Algun dels límits laterals o ambdós són infinits.
Vegem doncs exactament cada cas:
- Estem en el cas anterior, discontinuïtat inevitable.
- Es compleix que : $$\displaystyle \lim_{x \to a^-}f(x)= \pm \infty$$ i/o $$\displaystyle \lim_{x \to a^+}f(x)= \pm \infty$$ i la funció està definida en $$x=a$$ (Independentment del seu valor).
En aquests casos apareixen les asímptotes verticals. Per saber més sobre aquestes podeu consultar el tema de representació gràfica.
Vegem un exemple:
Prenguem la funció $$$ \displaystyle f(x)=\left \{ \begin{array}{rcl} \frac{1}{x} & \mbox{ si } x \neq 0 \\ 1 & \mbox{ si } & x=0 \end{array} \right.$$$ podem veure que en el zero segurament tindrem algun problema de continuïtat, així que mirem què passa amb la continuïtat de la funció en aquest punt: $$$\displaystyle \begin{array}{l} \lim_{x \to 0^-} f(x)= \lim_{x \to 0^-} \frac{1}{x}=\frac{1}{0^-}=-\infty \\ \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}\frac{1}{x}=\frac{1}{0⁺}= \infty \\ f(0)=1 \end{array}$$$ Per tant tenim una discontinuïtat essencial en el punt $$x=0$$.
Podem veure una representació gràfica de la funció:
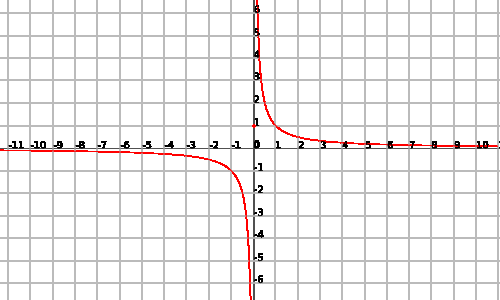
Atenció! La funció $$\displaystyle f(x)=\frac{1}{x}$$ no presenta discontinuïtat essencial ja que la funció és contínua.
La discontinuïtat la tindríem al punt $$x=0$$, però aquest no és del domini de la funció, així que no es pot definir la discontinuïtat.
No obstant això, la funció sí que té una asímptota vertical en $$x=0$$ i té un comportament anàleg al de la discontinuïtat essencial.
