En aquest apartat introduirem el mètode més general per al càlcul de volums en l'espai. De la mateixa manera que fèiem en el cas de superfícies en el pla, el mètode per calcular volums és integrar la funció $$1$$ (integral en sentit de $$\mathbb{R}^3$$, és a dir, integral triple) en el domini determinat, en aquest cas el nostre volum.
Per tant, una altra vegada la dificultat es troba en com parametritzar aquest volum, més que en com integrar.
Si volem conèixer el volum de la regió $$V$$, tindrem:
$$$\text{Vol}(V)=\iiint_V 1 \ dx \ dy \ dz$$$
De la mateixa manera que en integrals dobles, de vegades ens és més fàcil fer un canvi de coordenades. En aquest cas, haurem de multiplicar per el determinant de la matriu jacobiana. A continuació presentem els canvis (i els seus determinants) més típics en el càlcul de volums: les coordenades esfèriques i les coordenades cilíndriques:
-
Esfèriques
$$$ \begin{array}{l} x=r\cdot\sin\theta\cdot\cos\varphi \\ y=r\cdot\sin\theta\cdot\sin\varphi \\ z=r\cdot\cos\theta \end{array} \quad \text{ amb } \quad \det=r^2\sin\theta$$$
-
Cilíndriques
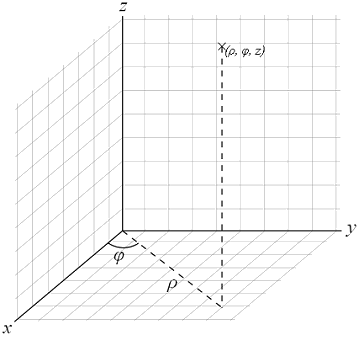
$$$ \begin{array}{l} x=r\cdot\cos\varphi \\ y=r\cdot\sin\varphi \\ z=z \end{array} \quad \text{ amb } \quad \det=r$$$
Per exemple, anem a calcular el volum delimitat pel paraboloide d'equació $$x^2+y^2=z$$ i el pla $$z=1$$.
Per la simetria del problema considerarem coordenades cilíndriques. Tenim:
$$$ \begin{array}{l} x=r\cdot\cos\varphi \\ y=r\cdot\sin\varphi \\ z=z \end{array} \quad \text{ amb } \quad \begin{array}{l} r\in[0,\sqrt{z}] \\ \theta\in[0,2\pi] \\ z\in[0,1] \end{array}$$$
Tenint en compte que el determinant del canvi és $$r$$, tenim:
$$$ \begin{array}{rl} \text{Vol}=&\iiint_V 1 \ dx \ dy \ dz =\int_0^1 \int_0^{2\pi} \int_0^{\sqrt{z}} r \ dr \ d\theta \ dz =\int_0^1 \int_0^{2\pi} \Big[ \dfrac{r^2}{2} \Big]_0^{\sqrt{z}} \ d\theta \ dz \\ =& \int_0^1 \int_0^{2\pi} \dfrac{z}{2} \ d\theta \ dz = \int_0^1 \pi\cdot z \ dz=\pi \Big[ \dfrac{z^2}{2} \Big]_0^1 = \dfrac{\pi}{2} \end{array}$$$

