In this section we will introduce the most general method for the calculation of volumes in space. In the same way as we did in the case of surfaces on the plane, the method to calculate volumes is to integrate the function $$1$$ (integral in the sense of $$\mathbb{R}^3$$, or, triple integral) in a certain domain, in this case our volume.
Therefore, the difficulty is again how we parametrize this volume more than the integration itself.
If we want to know the volume of the region $$V$$, we will have:
$$$\text{Vol}(V)=\iiint_V 1 \ dx \ dy \ dz$$$
In the same way as with double integrals, sometimes it is easier to do a change of coordinates. In such a case, we will have to multiply by the determinant of the Jacobian matrix. We introduce more typical changes (and the determinants) in the calculation of volumes, the spherical ones and the cylindrical ones:
-
Spherical
$$$ \begin{array}{l} x=r\cdot\sin\theta\cdot\cos\varphi \\ y=r\cdot\sin\theta\cdot\sin\varphi \\ z=r\cdot\cos\theta \end{array} \quad \text{ with } \quad \det=r^2\sin\theta$$$
-
Cylindrical
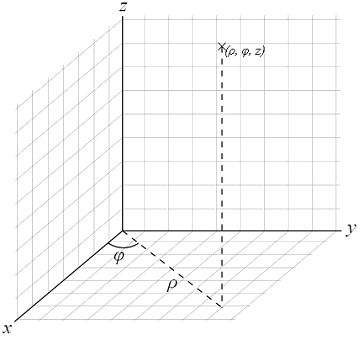
$$$ \begin{array}{l} x=r\cdot\cos\varphi \\ y=r\cdot\sin\varphi \\ z=z \end{array} \quad \text{ with } \quad \det=r$$$
For example, we are going to calculate the volume delimited by the paraboloid with equation $$x^2+y^2=z$$ and the plane $$z=1$$.
For the symmetry of the problem we will consider cylindrical coordinates. We have:
$$$ \begin{array}{l} x=r\cdot\cos\varphi \\ y=r\cdot\sin\varphi \\ z=z \end{array} \quad \text{ with } \quad \begin{array}{l} r\in[0,\sqrt{z}] \\ \theta\in[0,2\pi] \\ z\in[0,1] \end{array}$$$
Taking into account that the determinant of the change is $$r$$, we have:
$$$ \begin{array}{rl} \text{Vol}=&\iiint_V 1 \ dx \ dy \ dz =\int_0^1 \int_0^{2\pi} \int_0^{\sqrt{z}} r \ dr \ d\theta \ dz =\int_0^1 \int_0^{2\pi} \Big[ \dfrac{r^2}{2} \Big]_0^{\sqrt{z}} \ d\theta \ dz \\ =& \int_0^1 \int_0^{2\pi} \dfrac{z}{2} \ d\theta \ dz = \int_0^1 \pi\cdot z \ dz=\pi \Big[ \dfrac{z^2}{2} \Big]_0^1 = \dfrac{\pi}{2} \end{array}$$$

