Funciones hay de muchos tipos y formas: funciones periódicas, definidas a trozos, crecientes, decrecientes, cóncavas, convexas, ... Pero entre todas ellas, las podemos clasificar en dos conjuntos más elementales: funciones continuas y funciones no continuas.
Vulgarmente se dice que una función es continua si es posible dibujarla sin tener necesidad de levantar el lápiz del papel y por lo tanto, dibujarla con un solo trazado.
Matemáticamente la definición es un poco más elaborada.
Consideremos una función $$f(x)$$. Diremos que es continua en el punto $$x=a$$ si se cumple que los límites laterales de $$f(x)$$ en $$x=a$$ coinciden con el valor de la función en $$x=a$$: $$$\displaystyle \lim_{x \to a^+} f(x)=\lim_{x \to a^-}f(x)= f(a)$$$ En la siguiente gráfica observamos una función continua.
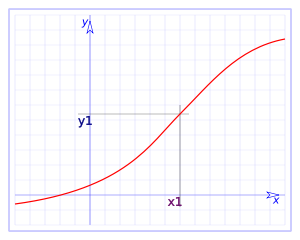
y podemos ver que los límites laterales coincidirán con el valor de la función en el punto $$x1$$, $$f (x1) = y1$$.
Veamos algunos ejemplos:
Tomamos la función $$f(x) = e^{-x^2}$$ y miremos la continuidad de la función en el punto $$x=0$$: $$$\displaystyle \begin{array} {l} \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+} e^{-x^2}= e^0= 1 \\ \lim_{x \to 0^-}f(x)=\lim_{x \to 0^-} e^{-x^2}= e^0= 1\end{array}$$$ y como los límites coinciden con el valor de la función en el cero: $$f(0)=e^0=1$$, entonces la función es continua en el cero.
Para ver un ejemplo de función no continua en un punto, tomemos la función $$\displaystyle f(x)=\left\{\begin{array}{rcl} x & \mbox{ si } & x \neq 2 \\ 0 & \mbox{ si } & x = 2\end{array}\right.$$ , y miremos la continuidad en $$x$$=2. Entonces observamos que: $$$\displaystyle \begin{array}{l} \lim_{x \to 2^+}f(x) = \lim_{x \to 2^+} x =2 \\ \lim_{x \to 2^-}f(x)=\lim_{x \to 2^-}x=2 \end{array} $$$ y si evaluamos la función en $$x=2$$ tenemos que $$f(2)=0$$, por lo que la función no es continua en el punto $$x=2$$.
