Definimos una función $$f(x)$$ continua si cumple que para todo punto de su dominio, la función es continua en ese punto. En una escritura más formal: $$$\displaystyle \mbox{ Para todo } x=a \mbox{ perteneciente a } Dom(f) , \lim_{x \to a^{\pm}} f(x)=f(a)$$$ Observamos que en una función continua tenemos continuidad y continuidad lateral en todos los puntos.
Atención: esta definición no es equivalente a la de "una función es continua si se puede dibujar sin levantar el lápiz del papel".
Observemos el siguiente ejemplo para mostrar las diferencias:
Tomemos la función $$\displaystyle f(x)=\frac{1}{x}$$. Si la representamos gráficamente tenemos:
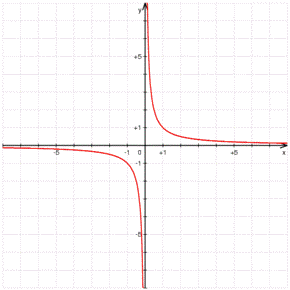
y podemos observar que tenemos dos ramas distintas que no están conectadas, por lo que podemos pensar que la función no es continua.
Esta función cumple la definición de continuidad que hemos dado, ya que para todo punto se cumple la definición, pero uno puede pensar que en $$x=0$$ pueda haber algún problema:
Los límites laterales no coinciden: $$$\displaystyle \begin{array} {l} \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}\frac{1}{x}=+ \infty \\ \lim_{x \to 0^-}f(x) = \lim_{x \to 0^-}\frac{1}{x}= -\infty \end{array}$$$ pero es que la función no está definida en el punto cero, por lo que no lo podemos comparar con el valor de $$f(0)$$.
Si nos fijamos, en la definición hablamos de continuidad en todos los puntos de su dominio y el cero no forma parte del dominio de esta función, así que no tiene sentido hablar de continuidad en este punto.
Por consiguiente, la función aun estar separada en dos ramas, es continua.
