We define a continuous function $$f(x)$$ if it satisfies that for any point of its domain, the function is continuous at this point. In a more formal way: $$$\displaystyle \mbox{ For all } x=a \mbox{ belonging to } Dom(f) , \lim_{x \to x^{\pm}} f(x)=f(a)$$$ We observe that in a continuous function we have continuity and side continuity in each and every point.
Attention: this definition is not equivalent to that of "a function is continuous if it is possible to draw it without raising the pencil from the paper".
Let's observe the following example to show the difference:
Let's take the function $$\displaystyle f(x)=\frac{1}{x}$$. If we represent it graphically we have the graph:
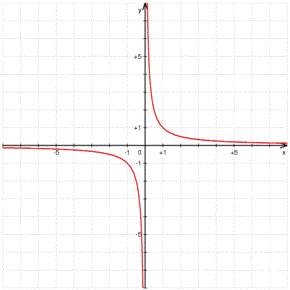
and we can observe that we have two different branches that are not connected, from that we can think that the function is not continuous.
This function satisfies the definition of continuity that we have given, if at any point the definition is satisfied, but one can think that at $$x=0$$ there could be some problem:
The side limits do not coincide: $$$\displaystyle \begin{array} {l} \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}\frac{1}{x}=+ \infty \\ \lim_{x \to 0^-}f(x) = \lim_{x \to 0^-}\frac{1}{x}= -\infty \end{array}$$$ but the fact is that the function is not defined at point zero, for we cannot compare with the value of $$f(0)$$.
Note that the definition of continuity is about all the points that are in the domain of the function, and not about the points that are outside the domain.
Consequently, the function in the example has two separated branches, both of them continuous.
