What is a triangle?

A triangle is a three-sided polygon determined by three segments of three straight lines that cross one another, i.e., the sides. The points where these segments cross, and that obviously will never be aligned, are named apexes.
Basic elements of the triangle
- Height: each of the perpendiculars drawn from one side to the opposite apex.
- The perpendicular bisectors of a triangle are each of the perpendiculars of its sides from their mid-points.
- Median of a triangle: each of the straight lines drawn from the middle point of one side to the opposite apex.
- The bisectors are the straight lines that divide each of the angles of the triangle in half.
Types of centers of a triangle
Geometrically, several centers can be defined in a triangle:
Barycenter
The point that is in the intersection of the medians and is equivalent to the gravity center.
Circumcenter
The center of the circumscribed circumference, the one that passes through the three apexes of the triangle. It is in the intersection of the perpendicular bisectors of the sides. Furthermore, the circumscribed circumference contains the intersection points of the perpendicular bisector of every side with the bisectors that pass through the opposite apex.
Incenter
The center of the inscribed circumference, which is the tangent to the sides of the triangle. We find it in the intersection of the bisectors of the angles.
Orthocenter
It is the point that is in the intersection of the height.
Excenters
The centers of the excircles, which are tangents to the sides of the triangle. We find them in the intersection of an interior bisector and two exterior bisectrors of the angles.
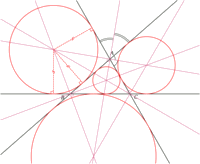
The only case where all the centers are the same is in the case of the equilateral triangle (all the sides of which are equal).
In particular, the orthocenter, the barycenter and the circumcenter are always aligned and the line through them is called Euler's line.





