Let's consider the graph of the following function $$f(x)=x^2$$:

We observe that any number $$x$$ and its opposite $$-x$$ have the same image. In this case we say that the function is a pair.
A function $$f$$ is a pair if for any $$x$$ in the domain we have: $$$f(x)=f(-x)$$$
Note that even functions are symmetrical with regard to the vertical axis.
Let's consider now the function $$f(x)=x^3$$:
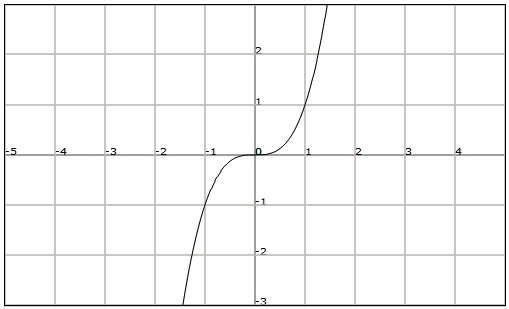
We know that any number $$x$$ and its inverse $$-x$$ have inverse images. In this case we say that the function $$f$$ is odd.
A function $$f$$ is odd if for any $$x$$ in the domain we have:$$$f(x)=-f(-x)$$$
Given following functions, decide which of them are even or odd: $$$\displaystyle f(x)=\frac{1}{x} \mbox{ and } g(x)=x^2-2$$$
Let's verify if the functions are even: $$$f(x)=f(-1) \Longleftrightarrow \displaystyle \frac{1}{x}=\frac{1}{-x} \Longleftrightarrow 1= -1 !! \\ g(x)=g(-x) \Longleftrightarrow x^2-2=(-x)^2-2=x^2-2 \mbox{ OK }$$$
Let's verify if the function $$f$$ is odd ($$g$$ will not be odd since it is an even function): $$$\displaystyle f(x)=-f(-x) \Longleftrightarrow \frac{1}{x}=-\frac{1}{-x}=\frac{1}{x} \mbox{ OK }$$$
Therefore the function $$f$$ is odd, and the function $$g$$ is a pair.
