Observe the function of the previous example. The maximum value that the images take is $$1$$. We will say that the function is bounded from above by $$1$$.
A function $$f$$ is bounded from above if there is a real number $$K$$ such that, for every $$x$$ belonging to the domain of $$f$$, $$f (x) \leq K$$. We will say that $$K$$ is an upper bound of the function.
We can now realize that the minimum value taken by the images is 0. We say that the function is bounded below.
A function $$f$$ is bounded from below if there is a real number $$K'$$ such that, for every $$x$$ belonging to the domain of $$f$$, $$f (x) \geq K'$$. We will say that $$K'$$ is a lower bound of the function.
Note that if $$K$$ is an upper bound of a function, then any other number greater than $$K$$ also is an upper bound. Also, if $$K'$$ is a lower bound of the function, then any other number smaller than $$K'$$ is a lower bound.
Indicate if the function of the graph is bounded, and find the upper and lower bound if they exist.
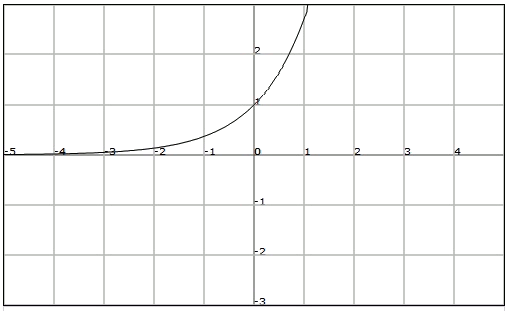
We observe that the function is bounded from below, but it is not bounded from above.
Therefore we will say that the function it is not bounded, though it will have a lower bound in $$K = 0$$.
