A very powerful tool in integral calculus is Green's theorem. Let's consider a vector field $$F(x,y)=(P(x,y),Q(x,y))$$, $$C$$ being a closed curve in the plane and $$S$$ the interior surface delimited by the curve.
Then: $$$\int_C F \ dr=\iint_S\big( Q_x-P_y \big) \ dx \ dy$$$
The application in the calculation of areas is the following one. We will think such a field being $$Q_x-P_y=1$$.Then the term on the right is only the area of the enclosure $$S$$. Therefore, we will be able to calculate it by doing one line integral on the border of the enclosure.
There are many fields that satisfy the property $$Q_x-P_y=1$$, but the most used are:
- $$F(x,y)=(0,x)$$
- $$F(x,y)=(-y,0)$$
- $$F(x,y)=(-y,x)$$
For example, we are going to calculate the area delimited by the parametric curve: $$$\alpha(\theta)=(3\sin(2\theta)\cdot\cos(\theta),3\sin(2\theta)\cdot\sin(\theta))$$$
with $$\theta\in\big[0,\dfrac{\pi}{2}\big]$$.
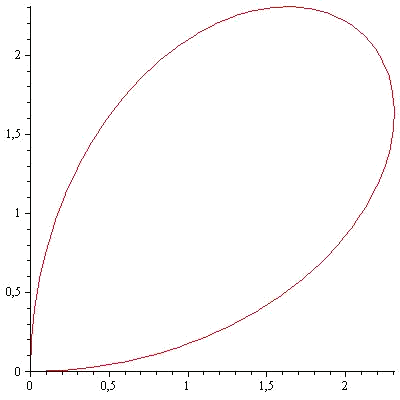
Now we take the vector field $$F(x,y)=(0,x)$$ and integrate the field along the curve $$\alpha(\theta)$$. Let's calculate: $$$ \alpha'(\theta)=(6\cos(2\theta)\cdot\cos(\theta)-3\sin(2\theta)\cdot\sin(\theta),6\cos(2\theta)\cdot\sin(\theta)-3\sin(2\theta)\cdot\cos(\theta))$$$
and we have:
$$$ \begin{array}{rl} \text{Area}=& \iint_D 1 \ dx \ dy=\int_C F \ dr = \int_0^{\frac{\pi}{2}} F(\alpha(t))\cdot\alpha'(t) \ dt \\ =& \int_0^{\frac{\pi}{2}} (0,3\sin(2t)\cdot\sin(t)) \cdot (6\cos(2t)\cdot\cos(t)-3\sin(2t)\cdot\sin(t), \\ & \quad \quad \quad \quad 6\cos(2t)\cdot\sin(t)-3\sin(2t)\cdot\cos(t)) \ dt \\ =& \int_0^{\frac{\pi}{2}} 3\sin(2t)\cos(t)\cdot (6\cos(2t)\cdot\sin(t)-3\sin(2t)\cdot\cos(t)) \ dt \\ = & 18\int_0^{\frac{\pi}{2}} \cos(t)\cos(2t)\sin(t)\sin(2t) \ dt + 9\int_0^{\frac{\pi}{2}} \sin^2(2t)\cos^2(2t) \ dt \\ =& 9\int_0^{\frac{\pi}{2}} \sin^2(2t)\cos(2t) \ dt + 9\int_0^{\frac{\pi}{2}} \sin^2(2t)\Big(\dfrac{1+\cos^2(2t)}{2}\Big) \ dt \\ =& \dfrac{9}{2}\Big[\dfrac{sin^3(2t)}{3})\Big]_0^{\frac{\pi}{2}}+ \dfrac{9}{2}\int_0^{\frac{\pi}{2}} \dfrac{1-\cos(4t)}{2} \ dt +\dfrac{9}{2}\int_0^{\frac{\pi}{2}} \sin^2(2t)\cos(2t) \ dt \\ =& \dfrac{9}{8}\cdot\pi \end{array}$$$
