In this section we will calculate areas determined by the graph of a function and the $$x$$ axis. We consider a real function $$f(x)$$ and its graph $$( x, f(x) )$$ in the plane:
.gif)
We want to calculate the colored area $$A$$. The area $$A$$, determined by the graph of the function, and a certain interval $$[a, b]$$ of the axis of $$x$$, is:
$$$A=\int_{a}^b f(x) \ dx$$$
We are going to calculate the area under the function $$f(x)=x^2$$ in the interval $$[-2,2]$$. Let's represent the function to have a geometric notion of the problem:
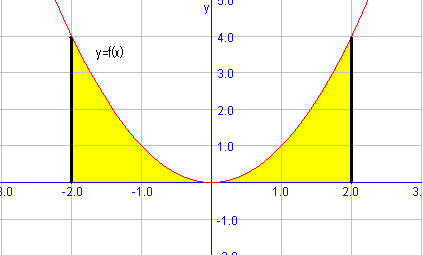
Therefore, we have to integrate the function in the interval that delimits the area: $$$A=\int_{-2}^2 x^2 \ dx=\Big[ \dfrac{x^3}{3} \Big]_{-2}^2= \dfrac{2^3}{3}-\dfrac{(-2)^3}{3}=\dfrac{8}{3}-\dfrac{-8}{3}= \dfrac{16}{3}\mathrm{u}^2$$$
Note: When we write $$u^2$$ we refer to the surface units.
We are going to calculate the area under the function $$f(x)=\sqrt{x}+\sin x$$ in the interval $$[0,4]$$. As we have done in the previous example, let's draw the function first of all:
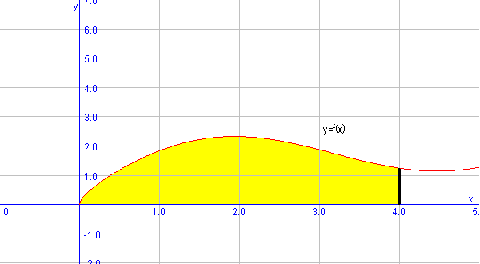
To calculate the area under $$f(x)$$, we have to integrate the above mentioned function in the corresponding interval: $$$ \begin{array}{rl} A=&\int_0^4(\sqrt{x}+\sin (x)) \ dx= \int_0^4\sqrt{x} \ dx + \int_0^4\sin(x) \ dx \\ =& \left[ \dfrac{x^{\frac{3}{2}}}{\dfrac{3}{2}} \right]_0^4+ [-\cos(x)]_0^4= \dfrac{2}{3}(8-0)-\cos(4)+1 \\ =& \dfrac{16}{3}+1.65=6.98 u^2 \end{array}$$$
