If now we want to determine the area delimited by two functions:
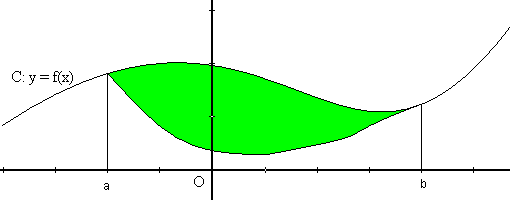
we will decompose the problem into two parts: first we will calculate the area delimited by the top graph and the $$x$$ axis and will subtract the area delimited by the lower graph.
So, if the top graph is $$(x,f(x))$$ and the lower one is $$(x,g(x))$$: $$$ A=\int_a^b f(x) \ dx - \int_a^b g(x) \ dx$$$
We are going to calculate the area delimited by the functions $$f(x)=\sin\Big( \dfrac{\pi}{2} \Big)$$ and $$g(x)=x$$ in the interval $$[0,1]$$. Let's draw the functions to know which is the top graph and which the bottom one:
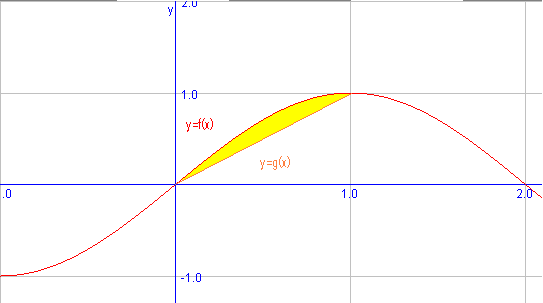
We see, then, that the top graph is $$f(x)$$ and the low one is $$g(x)$$. Therefore the area between two functions $$[-1,1]$$ is:
$$$ \begin{array}{rl} A =&\int_0^1 f(x)\ dx-\int_0^1 g(x) \ dx = \int_0^1 \sin\Big(\dfrac{\pi}{2}x\Big) \ dx- \int_0^1 x \ dx \\ =& \dfrac{2}{\pi}\Big[-\cos\Big(\dfrac{\pi}{2}x \Big)\Big]_0^1-\Big[\dfrac{x^2}{2}\Big]_0^1= \dfrac{2}{\pi}(0+1)-\dfrac{1}{2}=\dfrac{4-\pi}{2\pi}u^2 \end{array}$$$
