Límits finits
Començarem mostrant un petit resum de les propietats dels límits finits.
Suposem que $$\displaystyle\lim_{x \to \pm \infty}{f(x)}=a$$ i que $$\displaystyle\lim_{x \to \pm \infty}{g(x)}=b$$, llavors es compleix que:
- $$\displaystyle\lim_{x \to \pm \infty}{f(x) \pm g(x)}=\displaystyle\lim_{x \to \pm \infty}{f(x)} \pm \displaystyle\lim_{x \to \pm \infty}{g(x)}=a \pm b$$
- $$\displaystyle\lim_{x \to \cdot \infty}{f(x) \pm g(x)}=\displaystyle\lim_{x \to \pm \infty}{f(x)} \cdot \displaystyle\lim_{x \to \pm \infty}{g(x)}=a \cdot b$$
- Si $$b \neq 0$$, $$\displaystyle\lim_{x \to \cdot \infty}{\frac{f(x)}{g(x)}}=\frac{\displaystyle\lim_{x \to \pm \infty}{f(x)}}{\displaystyle\lim_{x \to \pm \infty}{g(x)}}=\frac{a}{b}$$
- Si $$f(x)>$$, $$\displaystyle\lim_{x \to \pm \infty}{f(x)^{g(x)}}=\displaystyle\lim_{x \to \pm \infty}{f(x)^{\displaystyle\lim_{x \to \pm \infty}{g(x)}}}=a^b$$
- Si $$n$$ imparell o si $$n$$ parell i $$f(x)\geqslant0 \Rightarrow \displaystyle\lim_{x \to \pm \infty}{\sqrt[n]{f(x)}}=\sqrt[n]{\displaystyle\lim_{x \to \pm \infty}{f(x)}}=\sqrt[n]{a}$$
- Si $$\alpha >0$$ i $$f(x)>0$$, $$\displaystyle\lim_{x \to \pm \infty}{ \log_{\alpha}f(x)}=\log_{\alpha}\Big(\displaystyle\lim_{x \to \pm \infty}{f(x)}\Big)=\log_{\alpha}a$$
Si$$\displaystyle\lim_{x \to {+} \infty}{f(x)}=3$$ i $$\displaystyle\lim_{x \to {+} \infty}{g(x)}=-5$$ llavors:
- $$\displaystyle\lim_{x \to {+} \infty}{f(x)+g(x)}=3-5=-2$$
- $$\displaystyle\lim_{x \to {+} \infty}{f(x)-g(x)}=3-(-5)=8$$
- $$\displaystyle\lim_{x \to {+} \infty}{f(x) \cdot g(x)}=3 \cdot (-5)=-15$$
- $$\displaystyle\lim_{x \to {+} \infty}{f(x)^g(x)}=3^{-5}=\frac{1}{3^5}=\frac{1}{243}$$
- $$\displaystyle\lim_{x \to {+} \infty}{g(x)^{f(x)}}$$ no existeix perquè $$g(x) < 0$$ per valors grans de $$x$$.
- $$\displaystyle\lim_{x \to {+} \infty}{\sqrt[3]{g(x)}}=\sqrt[3]{-5}=-\sqrt[3]{5}$$
- $$\displaystyle\lim_{x \to {+} \infty}{\sqrt{g(x)}}$$ no existeix perquè $$g(x) < 0$$ per valors grnas de $$x$$.
Límits infinits
Comencem definint què és un límit infinit d'una funció $$f(x)$$:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)}=+\infty \Longleftrightarrow \mbox{ donat un nombre arbitrari } k, \mbox{ podem trobar un altre nombre } h$$$
$$$ \mbox{ tal que si } x>h \mbox{ aleshores } f(x)>k$$$
Intuitivament, ens ve a dir que podem aconseguir que $$f(x)$$ sigui tan gran com vulguem només escollint un valor prou gran de $$x$$.
Anàlogament es defineix:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)}=-\infty \Longleftrightarrow \mbox{ donat un nombre arbitrari } k, \mbox{ podem trobar un altre nombre } h$$$
$$$ \mbox{ tal que si } x>h \mbox{ aleshores } f(x)<-k$$$
i per límits quan $$x$$ tendeix a menys infinit:
$$$\displaystyle\lim_{x \to {-} \infty}{f(x)}=+\infty \Longleftrightarrow \mbox{ donat un nombre arbitrari } k, \mbox{ podem trobar un altre nombre } h$$$
$$$\mbox{ tal que si } x<-h \mbox{ aleshores } f(x)>k$$$
$$$\displaystyle\lim_{x \to {-} \infty}{f(x)}=-\infty \Longleftrightarrow \mbox{ donat un nombre arbitrari } k, \mbox{ podem trobar un altre nombre } h$$$
$$$\mbox{ tal que si } x<-h \mbox{ aleshores } f(x)<-k$$$
Vegem tres exemples bàsics de funcions que tendeixen a infinit:
Potènica $$k$$-èssima: si $$k>0, \displaystyle\lim_{x \to {+}\infty}{x^k}=+\infty$$
i en particular $$\displaystyle\lim_{x \to {+}\infty}{p\cdot x^k}=sign(p) \cdot \infty$$ , on $$p$$ és un valor real diferent de zero.
D'aquest punt, deduïm que les funcions polinòmiques tendeixen a infinit conforme $$x$$ es fa gran.
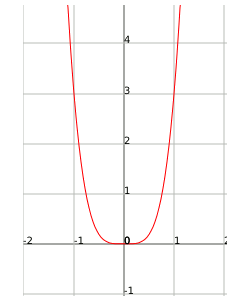
En aquest exemple podem veure la funció $$f(x)=3x^4$$. Quan $$x$$ es fa gran, la funció creix a l'infinit.
Exponencial: si $$a>1, \displaystyle\lim_{x \to {+}\infty}{a^x}=+\infty$$
i de la mateixa manera si $$a>1, \displaystyle\lim_{x \to {+}\infty}{p \cdot a^x}=sign(p) \cdot \infty$$ .
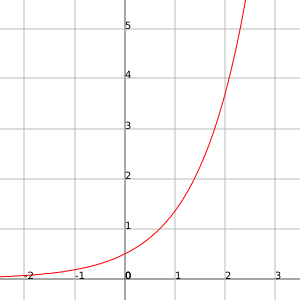
Un exemple per aquest cas és la funció $$f(x)=\dfrac{1}{2}e^x$$. Tendeix a infinit quan $$x$$ tendeix a infinit.
Logarítmiques: si $$a>1, \displaystyle\lim_{x \to {+}\infty}{\log_{a}x}=+ \infty$$
anàlogament si $$a>1 \displaystyle\lim_{x \to {+}\infty}{\log_{a}x}=sign(p) \cdot \infty$$.
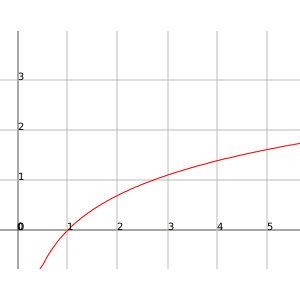
Per exemple, la funció $$f(x)= \log_{e}x=\ln x$$. Aquesta funció tendeix a l'infinit quan $$x$$ es fa gran molt lentament.
Aritmètica de l'infinit
Suposem que $$\displaystyle\lim_{x \to {+} \infty}{f(x)}=+\infty$$ i que $$\displaystyle\lim_{x \to {+} \infty}{g(x)}=+\infty$$, aleshores observem sense problemes que:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)+g(x)}=\displaystyle\lim_{x \to {+} \infty}{f(x)}+\displaystyle\lim_{x \to {+} \infty}{g(x)}=+\infty + \infty=+\infty$$$
$$$\displaystyle\lim_{x \to {+} \infty}{f(x) \cdot g(x)}=\displaystyle\lim_{x \to {+} \infty}{f(x)} \cdot \displaystyle\lim_{x \to {+} \infty}{g(x)}=(+\infty) \cdot (+\infty)=+\infty$$$
De totes maneres, tindrem problemes quan ens trobem amb situacions com la següent:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)-g(x)}=\displaystyle\lim_{x \to {+} \infty}{f(x)}-\displaystyle\lim_{x \to {+} \infty}{g(x)}=(+\infty)-(+\infty)$$$
ja que restar infinit menys infinit ens dóna una indeterminació.
De la mateixa manera, podríem plantejar-nos les propietats entre una funció amb límit infinit i una amb límit finit.
Vegem doncs, una petita taula que ens mostrarà com s'ha d'operar l'infinit amb altres infinits i amb límits finits:
| SUMES | PRODUCTES |
| $$(+\infty)+a=+\infty$$ | $$(+\infty)\cdot(+\infty)=+\infty$$ |
| $$(+\infty)+(+\infty)=+\infty$$ | $$(+\infty)\cdot(-\infty)=-\infty$$ |
| $$(-\infty)+a=-\infty$$ | $$(+\infty)\cdot a=sign(a) \cdot \infty$$ |
| $$(-\infty)+(-\infty)=-\infty$$ | $$(-\infty)\cdot a=-sign(a) \cdot \infty$$ |
| $$-(-\infty)=+\infty$$ | |
| DIVISIONS | POTÈNCIES |
| $$\frac{a}{\pm \infty}=0$$ | $$(+\infty)^{+\infty}=+\infty$$ |
| $$\frac{a}{0}=\pm \infty$$ if $$a\neq 0$$ | $$(+\infty)^{-\infty}=0$$ |
| $$\frac{\pm \infty}{0}=\pm \infty$$ | si $$a$$ > $$0$$ $$$(+\infty)^a= + \infty$$$ |
| $$\frac{0}{\pm \infty}=0$$ | si $$a$$ < $$0$$ $$$(+\infty)^a=0$$$ |
| si $$a\neq 0$$ $$$a^0=1$$$ | |
| si $$a$$ > $$1$$ $$$a^{+\infty}=+\infty \\ a^{-\infty}=0$$$ | |
| si $$0$$ <$$a$$ < $$1$$ $$$a^{+\infty}=0 \\ a^{-\infty}=+ \infty$$$ |
Aquestes operacions es poden realitzar després de trobar els límits de les funcions implicades.
No obstant les operacions que no estan en la taula poden produir indeterminacions, per exemple, són indeterminacions les següents expressions:
$$$(+\infty)-(+\infty) \\ 0 \cdot (\pm \infty) \\ \frac{0}{0} \\ (+\infty)^0 \\ 1^{\pm \infty} \\ 0^0 \\ \frac{\pm \infty}{\pm \infty}$$$
