Expresar y operar con tiempo en horas, minutos y segundos

Ejemplo

Expresemos diversos valores en minutos y segundos:

$4$ horas en minutos es: $$4\text{horas}=4\text{horas}\cdot \frac{60\text{minutos}}{1\text{hora}}=4\cdot 60\text{minutos}=240\text{minutos}$$

Media hora en segundos: $$\frac{1}{2}\text{hora}=\frac{1}{2}\text{hora}\cdot \frac{60\text{minutos}}{1\text{hora}}\frac{60\text{segundos}}{1\text{minuto}}=$$ $$=\frac{60\cdot 60}{2}\text{segundos}=1800\text{segundos}$$

Ejemplo

Cuando tenemos un minuto y medio por ejemplo, escribiremos $1$ minuto y la mitad de este que son $30$ segundos, es decir: $1^{\prime }{30}^{″}$.

Si queremos escribir $7$ horas y media pues, escribiremos $7$ y la media hora en minutos. Dado que una hora son $60$ minutos la mitad de una hora serán la mitad de $60$ minutos que son $30$.

Así, siete horas y media son $7h{30}^{\prime }$.

Ejemplo

También podemos hacer el proceso inverso, es decir, dados un número de segundos determinar qué número de minutos y/o horas son.

Por ejemplo, ¿cuántos minutos son $1020$ segundos?

$$1020\text{segundos}=1020\text{segundos}\cdot \frac{1\text{minuto}}{60\text{segundos}}=\frac{1020}{60}\text{minutos}=17\text{minutos}$$

Ejemplo

Supongamos que tenemos $68$ segundos.

A partir de ahora utilizaremos la notación estándar de minutos ${}^{\prime }$ y segundos ${}^{″}$ para agilizar la escritura y también acostumbrarnos a ella.

Usando factores de conversión nos da

$${68}^{″}={68}^{″}\cdot \frac{1^{\prime }}{{60}^{″}}=\frac{{68}^{\prime }}{60}=1,{13333}^{\prime }$$

Pero expresar ${68}^{″}$ como un número decimal de minutos no es demasiado útil. Lo que queremos hacer es expresarlo mejor por ejemplo como ${68}^{″}={60}^{″}+8^{″}=1^{\prime }{8}^{″}$ que son un minuto y ocho segundos.

Para poder expresarlo así, se debe tomar la parte entera del resultado, multiplicarla por $60$ y restarla a la cantidad original.

Esto es:

En el caso anterior el resultado era $1,13333$, cogemos la parte entera que es $1$.

La multiplicamos por $60$ y nos da $60$.

Ahora restamos este $60$ a la cantidad original que era $68$.

Nos da $8$.

Por lo tanto tenemos $1^{\prime }{8}^{″}$.

Ejemplo

Supongamos que tenemos $24355$ segundos. Expresémoslo en horas, minutos y segundos:

Primero lo pasamos a minutos

$${24355}^{″}={24355}^{″}\cdot \frac{1^{\prime }}{{60}^{″}}=\frac{{24355}^{\prime }}{60}={405.9166}^{\prime }$$

Por lo tanto, cogemos la parte entera de dicha división: es $405$ y lo multiplicamos por $60$: $$405\cdot 60=24300$$

Ahora, a la cantidad original le restamos este número, obteniendo $$24355-24300=55$$

Así pues, tenemos que ${24355}^{″}={405}^{\prime }{55}^{″}$

Ahora debemos expresar los ${405}^{\prime }$ en horas:

Mediante el factor de conversión: $${405}^{\prime }={405}^{\prime }\cdot \frac{1h}{{60}^{\prime }}=\frac{{405}^{\prime }}{60}=6,75h$$

Volvemos a hacer el proceso. Cogemos la parte entera que es $6$. La multiplicamos por $60$ y obtenemos $6\cdot 60=360$. A la cantidad original le restamos esta: ${405}^{\prime }-{360}^{\prime }=45$' Así pues, ${405}^{\prime }=6h{45}^{\prime }$ Por lo tanto ${24355}^{″}=6h{45}^{\prime }{55}^{″}$

Ejemplo

$750$ segundos, ¿cuántos minutos son?

Bueno tomemos $750$ y dividámoslos por $60$ $$\frac{750}{60}=12,5$$

$$750=12\text{minutos}+0,5\text{minutos}$$

Ahora, la forma más fácil de sacar los segundos que representan esos $0,5$ es multiplicándolo por $60$ ($0,5$ está en minutos y para representarlo en forma correcta necesitamos obtenerlo en segundos):

$0,5\cdot 60=30$ segundos. Este procedimiento es el que hemos explicado antes.

Finalmente tenemos que:

$750$ segundos $=12$ minutos y $30$ segundos.

Ejemplo

$$\begin{array}{ccccc}\alpha & =& 74h& {16}^{\prime }& {54}^{″}\\ \beta & =& 28h& {45}^{\prime }& {13}^{″}\end{array}$$ $$\alpha +\beta =(74h{16}^{\prime }{54}^{″})+(28h{45}^{\prime }{13}^{″})=102h{61}^{\prime }{67}^{″}$$

Así, nos damos cuenta que lo que se debe hacer una vez sumadas las cantidades es revisar que si los segundos sobrepasan $60$ los debemos expresar en minutos y sumarlos a los que ya tenemos. Y lo mismo con los minutos, que si sobrepasan de 60 también deberemos pasarlos a horas.

En el caso anterior tenemos ${67}^{″}$ que son $1^{\prime }{7}^{″}$. Por lo tanto reescribimos el resultado sumándole un minuto y dejando $7$ segundos. $$103h{62}^{\prime }{7}^{″}$$

Pero como tenemos más de $60$ minutos, escribimos una hora más y dejamos $2$ minutos (ya que tenemos ${62}^{\prime }$). Por lo tanto: $103h{2}^{\prime }{7}^{″}$ es la suma de esas dos cantidades.

Ejemplo

$$4^{\prime }{11}^{″}-2^{\prime }{47}^{″}$$ Dado que $11$ es menor que $47$, restamos un minuto a $4$ y añadimos $60$ segundos a $11$.La resta quedará: $$3^{\prime }{71}^{″}-2^{\prime }{47}^{″}=1^{\prime }{24}^{″}$$

Ejemplo

$$4h{23}^{\prime }{11}^{″}-2h{47}^{\prime }{27}^{″}$$

En este caso $27$ es mayor que $11$ por lo que restamos un minuto a $23$ que teníamos y le sumamos $60$ segundos a $11$ que teníamos. La resta ahora es: $$4h{22}^{\prime }{71}^{″}-2h{47}^{\prime }{27}^{″}$$

Pero ahora, nos damos cuenta que en los minutos vuelve a pasar lo mismo, que $47$ es mayor que $22$ minutos del original, por lo que le restamos $1$ hora al original y le sumamos $60$ minutos. La resta ahora es:

$$3h{82}^{\prime }{71}^{″}-2h{47}^{\prime }{27}^{″}=1h{35}^{\prime }{44}^{″}$$

Ejemplo

$$\frac{\begin{array}{ccc}3h& {12}^{\prime }& {45}^{″}\\ & \times & 3\end{array}}{\begin{array}{ccc}9h& {36}^{\prime }& {135}^{″}\end{array}}$$

Por lo tanto pasamos los ${135}^{″}$ a minutos: ${\displaystyle \frac{135}{60}}=2,25$ cogemos la parte entera y multiplicada por $60$ la restamos al $135$, es decir:

$$135-2\cdot 60=135-120=15$$

Así, debemos sumar $2$ minutos a los $36$ que ya teníamos y dejar ${15}^{″}$.

Por lo tanto el resultado es: $9h{38}^{\prime }{15}^{″}$.

Ejemplo

El siguiente ejemplo nos permite efectuar la división del tiempo $34h{28}^{\prime }{44}^{″}$ entre $4$.

• Paso 1 Dividimos las horas entre $4$. $$34=4\cdot 8+2$$

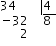
El resto es $2$, por lo tanto lo multiplicamos por $60$ y lo sumamos a los minutos. $$60\cdot 2=120$$ Los sumamos a $28$, $$120+28={148}^{\prime }$$

• Paso 2 Dividimos los minutos entre $4$.

$$148=4\cdot 37+0$$

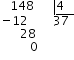
El resto es $0$, por lo que no hace falta sumarle nada a los segundos.

• Paso 3 Dividimos los segundos entre el número $4$. $$44=4\cdot 11+0$$

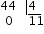
Por último escribimos el resultado: $8h{37}^{\prime }{11}^{″}$