Coordenadas de un punto en el plano
Veamos como se utilizan los vectores para asignar coordenadas a los puntos del plano.
Consideramos un punto fijo del plano $$O$$ (conocido como origen), y una base $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$ de $$V_2$$ (Espacio vectorial de dimensión 2).
Recordemos que una base de $$V_2$$ son dos vectores linealmente independientes. El conjunto formado por $$O$$ y $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$ constituye un sistema de referencia en el plano, ya que permite determinar la posición de cualquier otro punto del plano.
Esto se debe al hecho que cualquier otro punto $$P$$ del plano determina con el punto $$O$$ un vector $$\overrightarrow{OP}$$. Sean $$(p_1,p_2)$$ las componentes del vector en la base $$B$$. Entonces $$(p_1,p_2)$$ son las coordenadas del punto $$P$$ en el sistema de referencia $$R=\{O;\overrightarrow{u}, \overrightarrow{v}\}$$ y escribimos $$P =(p_1,p_2)$$.
El procedimiento para encontrar las coordenadas de un punto $$P$$ en un sistema de referencia dado es el siguiente:
-
A partir de los puntos $$O$$ i $$P$$ determinamos el vector $$\overrightarrow{OP}$$
-
Expresamos el vector $$\overrightarrow{OP}$$ como combinación lineal de los vectores de la base $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, es decir, $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$
- $$P=(p_1,p_2)$$
Expresar el punto $$P$$ del dibujo en el sistema de referencia $$R =\{O;\overrightarrow {u}, \overrightarrow{v}\}$$.
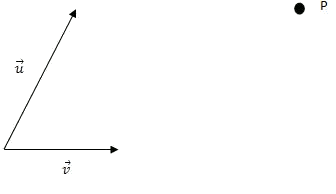
- Dibujamos el vector $$\overrightarrow{OP}$$:
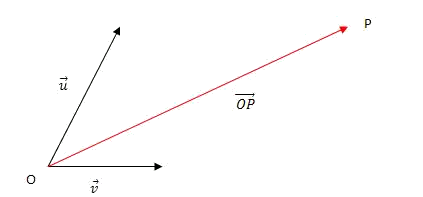
- Expresamos el vector $$\overrightarrow{OP}$$ como combinación lineal de los vectores de la base $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$:
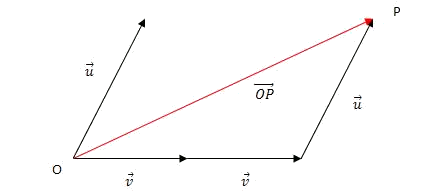
- Obtenemos $$\overrightarrow{OP}=\overrightarrow{u}+2\overrightarrow{v}$$ y por tanto las coordenadas del punto $$P$$ son $$P = (1 , 2)$$
De ahora en adelante consideraremos como sistema de referencia $$R$$ el formado por el origen de coordenadas $$O = (0, 0)$$ y la base canónica de $$V_2$$ $$B =\{\overrightarrow{i},\overrightarrow{j}\}$$.
Componentes de un vector determinado por dos puntos
Veamos ahora la forma de determinar las componentes de un vector si sabemos las coordenadas de sus extremos:
Sean $$P =(p_1,p_2)$$ y $$Q = (q_1,q_2)$$ dos puntos del plano, y sea $$\overrightarrow{PQ}$$ el vector que va de $$P$$ a $$Q$$. Entonces las componentes del vector $$\overrightarrow{PQ}$$ son $$\overrightarrow{PQ}=(q_1-p_1,q_2-p_2)$$.
Sean $$P = (2, 6)$$ y $$Q = (-3, 9)$$. Las componentes del vector $$\overrightarrow{PQ}$$ son:$$\overrightarrow{PQ}= (-3 - 2, 9 - 6) = (-5, 3)$$
Aplicar un vector a un punto
Dados un punto $$P$$ y un vector $$\overrightarrow{v}$$, el resultado de aplicar el vector al punto es un nuevo punto $$Q$$ situado en la dirección de $$\overrightarrow{v}$$ y a una distancia $$|\overrightarrow{v}|$$. (módulo del vector $$\overrightarrow{v}$$)
Las coordenadas de este nuevo punto $$Q$$ se calculan a partir de las de $$P =(p_1,p_2)$$ y $$\overrightarrow{v}=(v_1,v_2)$$ cómo: $$$Q = P +\overrightarrow{v}=(p_1+v_1,p_2+v_2)$$$
NOTA: Es muy importante tener presente que esta operación de "suma" sólo tiene sentido entre un punto y un vector. NUNCA debemos sumar dos puntos, y el resultado de sumar dos vectores es otro vector y no un punto!
Dada la siguiente figura, determinar las coordenadas del punto $$P$$ de la figura resultado de aplicar el vector $$\overrightarrow{v}$$ al punto $$A$$.
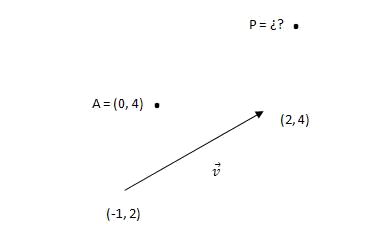
Empezamos calculando las componentes del vector $$\overrightarrow{v}$$:$$$\overrightarrow{v} = (2 - (-1), 4-2) = (3, 2)$$$ Como $$P$$ es el resultado de aplicar el vector $$\overrightarrow{v}$$ al punto $$A$$ se tiene, $$$P=A+\overrightarrow{v}=(0,4)+(3,2)=(3,6)$$$
Punto medio de un segmento
Consideremos ahora el segmento de extremos $$A = (a_1,a_2)$$ y $$B = (b_1,b_2)$$. Sea $$M =(m_1,m_2)$$ el punto medio de dicho segmento. Evidentemente dicho punto cumple que $$\overrightarrow{AB}=2\cdot \overrightarrow{AM}$$, o sea que $$(b_1-a_1,b_2-a_2)=2\cdot (m_1-a_1,m_2-a_2)$$
Separando componente a componente obtenemos: $$$\begin{array}{rcl} b_1-a_1 & = & 2 \cdot (m_1-a_1) \\ b_2-a_2 &=& 2\cdot (m_2-a_2) \end{array}$$$ y aislando tenemos: $$$\begin{array}{rcl} m_1 & = & \displaystyle \frac{a_1+b_1}{2}\\ m_2 &=& \displaystyle \frac{a_2+b_2}{2} \end{array}$$$ De forma que podemos calcular las coordenadas del punto medio de un segmento a partir de las coordenadas de sus extremos.
Dados los puntos $$A = (-3, 7)$$ y $$B = (1, 2)$$ encontrad el punto medio del segmento que determinan.
Aplicando las fórmulas anteriores tenemos: $$$\begin{array}{rcl} m_1 & = & \displaystyle \frac{a_1+b_1}{2}= \frac{-3+2}{2}=-1\\ m_2 &=& \displaystyle \frac{a_2+b_2}{2}=\frac{7+2}{2}=\frac{9}{2} \end{array}$$$ Por tanto el punto medio del segmento $$AB$$ es $$M = (-1, \displaystyle \frac{9}{2})$$
