In this section we are going to define the trigonometric functions. In the two previous sections, we have seen that given a right triangle $$ABC$$,we can calculate the sine, the cosine and the tangent (and its respective inverse ratios) by means of the quotient between two sides of the triangle. In this paragraph we want to go one step further and define the trigonometric functions. Given an angle $$x$$, to calculate its sine, for example, we can draw a right triangle, and name $$x$$ as one of its non-right angles. This way, once the triangle is drawn, and by using the previously given formulas, we can calculate the sine, the cosine and the tangent. Then, since this can be done for any angle $$x$$, we can define a function assigning the corresponding value to each angle $$x$$.
Thus, we define: $$y = sin (x)$$.
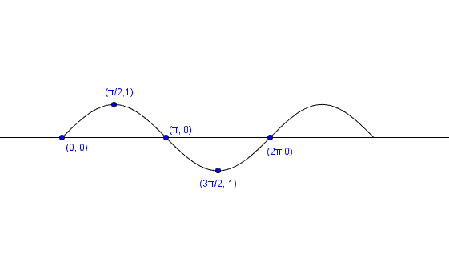
$$y$$ is equal to the sine of $$x$$.
Its inverse function is: $$x = \arcsin(y)$$
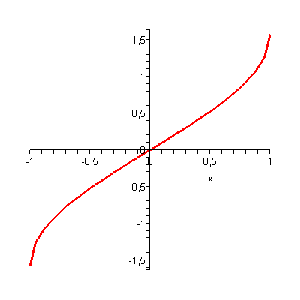
$$x$$ is the arc (of the circumference) which sine equals $$y$$, or also, that $$x$$ is the arcsine of $$y$$.
If $$y = \cos (x)$$
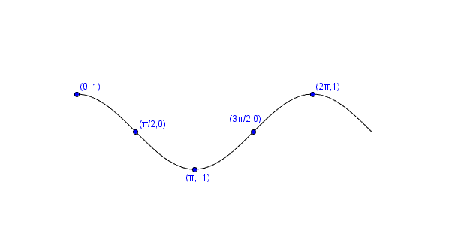
It is said that $$y$$ is equal to the cosine of $$x$$ and its inverse function is $$x = \arccos(y)$$.
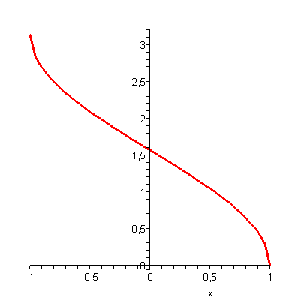
One says that $$x$$ is the arc which cosine is $$y$$, this is, $$x$$ is the arcsine of $$y$$.
If $$y = \tan (x)$$
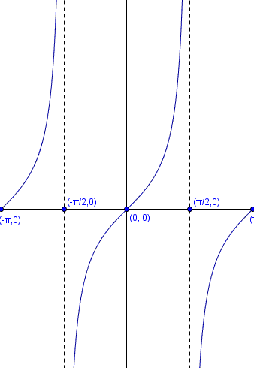
It is said that $$y$$ is equal to the tangent of $$x$$ and its inverse function is: $$x = \arctan(y)$$.

It is said that $$x$$ is the arc which tangent is $$y$$, or that $$x$$ is equal to the arctangent of $$y$$.
Note that the values of $$x$$ can be expressed both in radians and degrees.
