Trigonometric identities of other angles

Supplementary angles

Two angles are said to be supplementary if they add up to $$180^\circ$$.

For example, an angle of $$140^\circ$$ and one of $$40^\circ$$ are supplementary since: $$$140^\circ+ 40^\circ=180^\circ $$$

imagen

The sine, cosine and tangent of the supplementary angles have a certain relation. That is, if $$\alpha$$ and $$\beta$$ are two supplementary angles then we have:

  • $$\sin(\alpha)=\sin(\beta)$$

  • $$\cos(\alpha)=-\cos(\beta)$$

  • $$\tan(\alpha)=-\tan(\beta)$$

So we have that their sines are equal, and their cosine and their tangent are equal with opposed signs.

In the previous example, then, we have:

  • $$\sin(40^\circ)=\sin(140^\circ)$$

  • $$\cos(40^\circ)=-\cos(140^\circ)$$

  • $$\tan(40^\circ)=-\tan(140^\circ)$$

Angles that differ in $$180^\circ$$

Two angles $$\alpha$$ and $$\beta$$ are said to differ in $$180^\circ$$ if $$\alpha-\beta=180^\circ$$.

For example an angle of $$240^\circ$$ and one of $$60^\circ$$ differ in $$180^\circ$$, since: $$$240^\circ-60^\circ=180^\circ$$$

imagen

The sine, cosine and tangent of two angles that differ in $$180^\circ$$ are also related. If $$\alpha$$ and $$\beta$$ differ in $$180^\circ$$, we have:

  • $$\sin(\alpha)=-\sin(\beta)$$

  • $$\cos(\alpha)=-\cos(\beta)$$

  • $$\tan(\alpha)=\tan(\beta)$$

That is, the sine and the cosine have equal values but differ in their signs, while the tangent is equal.

In the previous example, therefore, we have:

  • $$\sin(240^\circ)=-\sin(60^\circ)$$

  • $$\cos(240^\circ)=-\cos(60^\circ)$$

  • $$\tan(240^\circ)=\tan(60^\circ)$$

Opposite angles

Two angles are said to be opposite angles if they add up to $$360^\circ$$. That is, $$\alpha$$ and $$\beta$$ are opposite angles if $$\alpha+\beta=360^\circ$$.

For example, an angle of $$330^\circ$$ and one of $$30^\circ$$ are opposite angles, since $$$330^\circ+30^\circ=360^\circ$$$

imagen

The sines, cosines and tangent of opposite angles are related in a similar way as the one we saw with the supplementary angles or those which differ in $$180^\circ$$. That is, if $$\alpha$$ and $$\beta$$ are opposite angles we have:

  • $$\sin(\alpha)=-\sin(\beta)$$

  • $$\cos(\alpha)=\cos(\beta)$$

  • $$\tan(\alpha)=-\tan(\beta)$$

That is, the sine and the tangent are equal but with different signs, and the cosine is exactly the same.

In the previous example we have:

  • $$\sin(330^\circ)=-\sin(30^\circ)$$

  • $$\cos(330^\circ)=\cos(30^\circ)$$

  • $$\tan(330^\circ)=-\tan(30^\circ)$$

Negative angles

An angle is negative if it goes clockwise, and it is symbolized by a minus sign.

For example, if there is an angle of $$30^\circ$$, but instead of going up it goes down, or clockwise, it is said that the angle is of $$-30^\circ$$.

The following illustration shows the negative angle $$-30^\circ$$:

imagen

If $$\alpha$$ is an angle, then we have the following identities:

  • $$\sin(-\alpha)=-\sin(\alpha)$$

  • $$\cos(-\alpha)=\cos(\alpha)$$

  • $$\tan(-\alpha)=-\tan(\alpha)$$

In short, the sine and the tangent of $$\alpha$$ and $$-\alpha$$ are the same but with different signs, and the cosine is exactly the same.

In the previous example we have:

  • $$\sin(-30^\circ)=-\sin(30^\circ)$$

  • $$\cos(-30^\circ)=\cos(30^\circ)$$

  • $$\tan(-30^\circ)=-\tan(30^\circ)$$

Angles greater than $$360^\circ$$

To find the sine, the cosine and the tangent of an angle greater than $$360^\circ$$, we have to do the following:

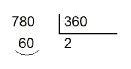
  1. The integer division of the given angle over $$360$$. For example, if the angle is $$780^\circ$$, then: imagen

  2. We then take the residual. In the previous example it is $$60^\circ$$.

  3. The sine, the cosine and the tangent of the given angle are that of the residual that has been obtained.

Going back to the previous example, we have:

  • $$\sin(780^\circ)=\sin(660^\circ)$$

  • $$\cos(780^\circ)=\cos(60^\circ)$$

  • $$\tan(780^\circ)=\tan(60^\circ)$$

Angles that differ in $$90^\circ$$

Two angles differ in $$90^\circ$$ if the result of subtracting them is $$90^\circ$$.

For example, an angle of $$160^\circ$$ and one of $$70^\circ$$, ja que: $$160^\circ- 70^\circ= 90^\circ$$. The following illustration shows it more clearly:

imagen

If it is true that two angles, $$\alpha$$ and $$\beta$$, differ in $$90^\circ$$ (that is to say, if $$\alpha-\beta=90^\circ$$) then:

  • $$\sin(\alpha)=\cos(\beta)$$

  • $$\cos(\alpha)=-\sin(\beta)$$

  • $$\tan(\alpha)=-\cot(\beta)$$

In the previous example we have that:

  • $$\sin(160^\circ)=\cos(70^\circ)$$

  • $$\cos(160^\circ)=-\sin(70^\circ)$$

  • $$\tan(160^\circ)=-\cot(70^\circ)$$

Angles that add up to $$270^\circ$$

Two angles $$\alpha$$ and $$\beta$$ add up $$270^\circ$$ if $$\alpha+\beta=270^\circ$$.

For example, an angle of $$70^\circ$$ and one of $$200^\circ$$, since $$70^\circ + 200^\circ=270^\circ$$.

In this case, $$\alpha$$ and $$\beta$$ satisfy the following identities:

  • $$\sin(\alpha)=-\cos(\beta)$$

  • $$\cos(\alpha)=-\sin(\beta)$$

  • $$\tan(\alpha)=\cot(\beta)$$

In the previous example, we have:

  • $$\sin(70^\circ)=-\cos(200^\circ)$$

  • $$\cos(70^\circ)=-\sin(200^\circ)$$

  • $$\tan(70^\circ)=\cot(200^\circ)$$

Angles that differ in $$270^\circ$$

Two angles $$\alpha$$ and $$\beta$$ differ in $$270^\circ$$ if, when subtracted, we obtain $$270^\circ$$: $$\alpha-\beta= 270^\circ$$.

An example is the angles of $$320^\circ$$ and $$50^\circ$$, since $$320^\circ-50^\circ=270^\circ$$.

When two angles $$\alpha$$ and $$\beta$$ differ in $$270^\circ$$ we have:

  • $$\sin(\alpha)=-\cos(\beta)$$

  • $$\cos(\alpha)=\sin(\beta)$$

  • $$\tan(\alpha)=-\cot(\beta)$$

In our example with the angle of $$320^\circ$$ and $$50^\circ$$, we have:

  • $$\sin(320^\circ)=-\cos(50^\circ)$$

  • $$\cos(320^\circ)=\sin(50^\circ)$$

  • $$\tan(320^\circ)=-\cot(50^\circ)$$