Right triangle resolution using trigonometric identities

Next we will explain how to find the sides and angles of a right triangle, if only some of them are known.

In the following pictures, the sides and angles in red are those that we are looking for, while those in black are the ones we know.

We are going to distinguish between the following cases, depending on what we know from the triangle:

  • The hypotenuse and a cathetus are known: In this case we have to find the remaining cathetus(side $$c$$) and two angles ($$B$$ and $$C$$).

    imagen

    • The angle $$B$$ is: $$B=\arcsin\Big( \dfrac{b}{a} \Big)$$
    • The angle $$C$$ is: $$C=90^\circ -B$$
    • The side $$c$$ is: $$c=a\cdot \cos(B)$$

  • Two cathetus are known: In this case we have to find the two angles ($$B$$ and $$C$$) and the hypotenuse (that is, the side $$a$$).

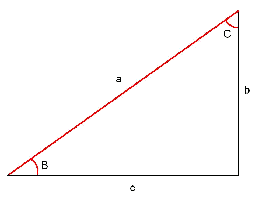
    imagen

    • The angle $$B$$ is: $$B=\arctan\Big( \dfrac{b}{c}\Big)$$
    • The angle $$C$$ is: $$C=90^\circ - B$$

    • The hypotenuse is: $$a=\dfrac{b}{\sin(B)}$$

      Also, it is possible to find it with the following identity: $$a=\sqrt{b^2+c^2}$$

  • The hypotenuse and an angle are known: In this case we will have to find another angle (that is, $$C$$) and the two cathetus (the sides $$b$$ and $$c$$).

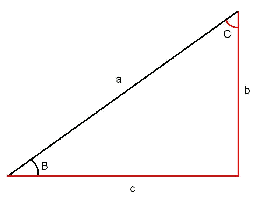
    imagen

    • The angle $$C$$ is: $$C=90^\circ -B$$
    • The side $$b$$ is: $$b=a\cdot\sin(B)$$

    • The side $$c$$ is: $$c=a\cos(B)$$

      Also, it is possible to find it by doing: $$c=\sqrt{a^2+b^2}$$

  • A cathetus and an angle are known: Here we will have to find the other angle ($$C$$), the hypotenuse (the side $$a$$) and the unknown cathetus (the side $$c$$).

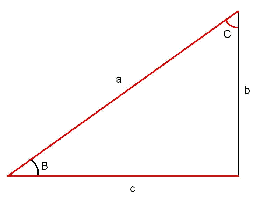
    imagen

    • The angle $$C$$ is: $$C=90^\circ -B$$
    • The side $$a$$ is: $$a=\dfrac{b}{\sin(B)}$$

    • The side $$c$$ is: $$c=\dfrac{b}{\tan(B)}$$

      Also: $$c=\sqrt{a^2+b^2}$$