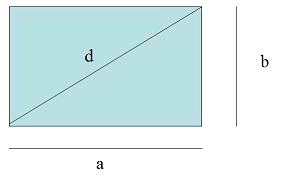
The area of the rectangle is: $$$A=a \cdot b$$$
Its perimeter is: $$$P=a+a+b+b=2a+2b=2(a+b)$$$
And, applying the Pythagorean theorem, its diagonal is: $$$d=\sqrt{a^2+b^2}$$$
Calculate the diagonal and the area of a rectangle of $$5 \ cm \times 10 \ cm$$.
-
Diagonal $$$ d^2=(5 \ cm)^2+(10 \ cm )^2 \\ d = \sqrt{25+100} \ cm \\ d= 5\sqrt{5} \ cm $$$
- Area $$$A= 5 \ cm \cdot 10 \ cm = 50 \ cm^2$$$
And so, the area of the rectangle is: $$50 \ cm^2$$.
