The area of the regular polygon is $$$A=\frac{Perimeter \cdot \ apothem}{2}$$$
The perimeter is: $$$P=n \cdot l$$$
with $$l$$ being the length of the radius and $$n$$ the number of sides.
Calculate the area of a hexagon of $$l=10 \ cm$$
- Using Pythagoras we find the apothem $$a$$, or the height of one of six equilateral triangles that form the hexagon.
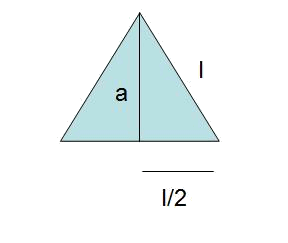
$$$l^2= a^a+ \Big(\frac{l}{2}\Big)^2 \\ a^2= l^2 \cdot \Big(1-\frac{1}{4}\Big) \\ a= \frac{\sqrt{3}}{2} \cdot l$$$
-
The area of one of the triangles: $$$A_{triangle}=\frac{l·a}{2} = l^2 \cdot \frac{\sqrt{3}}{4}= 25 \sqrt{3} \ cm^2$$$
- Finally, multiplying by $$6$$ we obtain the total area: $$$A_{hexagon}=150\sqrt{3} \ cm^2$$$
Note: To find areas of more complex irregular polygons, the philosophy will be the same: to break them down into triangles and to add the areas of the triangles.
