It is the resultant polyhedron after having made a parallel cut to the basis of a pyramid. The mentioned cut will be named a minor base.
-
Lateral faces will have now the shape of isosceles trapeze.
- The height will be the distance between basis.
The following figure is an example of a frustum of pyramid with pentagonal bases.
Calculate the area of a frustum of pyramid of basis squared with: $$$A_{basis}=16 \ m^2 \\ A_{minor \ basis}= 9 \ m^2 \\ height = 3$$$ To find the area of the trapeze sides, it is necessary to calculate the value of $$Ap$$, the apothem of the frustum of pyramid, or height of the trapeze:
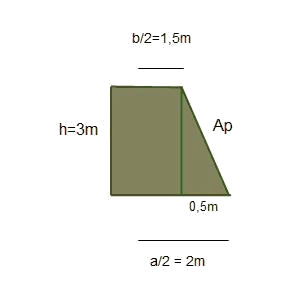
$$a$$ being the side of the basis and $$b$$ the side of the minor basis. Analyzing the triangle that remains, of basis $$0,5 \ m$$: $$$Ap^2=0,5^2+3^2 \\ Ap=3,04 \ m$$$
Now that we already have the apothem, we calcule the area of the side, $$$A_{lateral}=\Big(Perimetre _{basis}+Perimetre_{minor \ basis}\Big) \dfrac{Ap}{2} \\ A_{lateral}=(16+12) \cdot \dfrac{3,04}{2}=42,56 \ m^2$$$ And the entire area will be: $$$A_{total}=A_{laterals}+A_{basis}+A_{minor \ basis} \\ A_{total}=42,56+9+16=67,56 \ m^2$$$
To calculate the volume of the pyramidal frustum we will use the following expression ($$h$$ is the height, $$A$$ is the area of the basis and $$A'$$ the area of the minor basis) $$$V=\dfrac{h}{3}(A+A'+\sqrt{A\cdot A'})$$$
In the previous example the mentioned volume has a value of $$V=55,5 m^3$$.

