The tetrahedron is a figure formed by $$4$$ equilateral triangles.
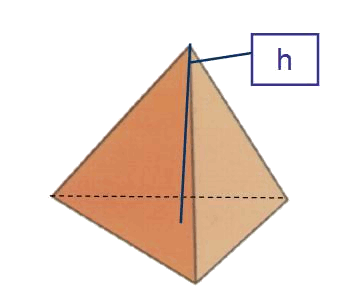
To calculate the area of the tetrahedron: $$$A_{tetrahedron}=4\cdot \dfrac{a\cdot h}{2}=2 \cdot a \cdot h$$$
The triangles that compose the tetrahedron are equilateral, so it is possible to express its height $$h$$ according to its base: $$$a^2=\Big(\dfrac{a}{2}\Big)^2+h^2 \\ h^2=a^2\Big(\dfrac{3}{4}\Big) \\ h= a \cdot \dfrac{\sqrt{3}}{2}$$$
And the area of the tetrahedron is: $$$A_{tetrahedron}=\dfrac{a \cdot a \cdot \dfrac{\sqrt{3}}{2}}{2}=\dfrac{a^2 \cdot \sqrt{3}}{4}=a^2 \cdot \sqrt{3}$$$
Finally, the expression of the volume of the regular tetrahedron is: $$$V=\dfrac{ \sqrt{2}}{12}\cdot a^3$$$
