The function that assigns to the independent variable $$x$$ the value of $$f (x) =\log_ax$$ is called logarithmic function of base $$a$$, where $$a$$ is a positive real number other than $$1$$.
We observe that if we apply the log to the exponential function base $$a$$ we obtain the identity function $$$\log_a(a^x)=x$$$ Similarly it is satisfied that $$$a^{\log_ax}=x$$$ Therefore the exponential and logarithmic functions are inverse functions.
Graph
As in case of the exponential functions, the graph of the logarithmic functions changes if the base is greater to or smaller than $$1$$.
Let's see it with $$f(x)=\log_2x$$ and $$h(x)=\displaystyle \log_{\frac{1}{2}}x$$.
It is remarkable that the logarithmic functions always go thorugh the point $$(1, 0)$$ since any number to the power $$0$$ is $$1$$.
$$f(x)=\log_2x$$
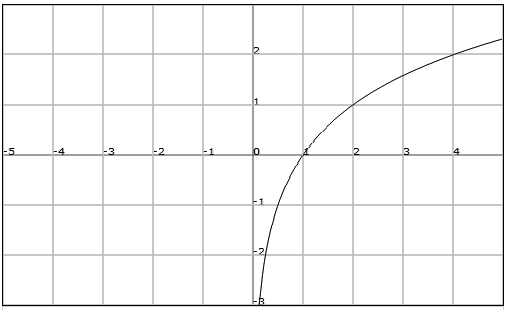
$$\displaystyle f(x)=\log_{\frac{1}{2}}x$$

Properties
From its graphic representation we observe that the logarithmic function satisfies the following properties:
- Domain: $$Dom (f) = (0,+\infty)$$
- Image: $$Im (f) = \mathbb{R}$$
- Bounds: It is not bounded.
- Intersection with the axes: It cuts the horizontal axis at $$x = 1$$. It does not cut the vertical axis.
- Continuity: It is continuous in its domain.
- Asimptotes: The straight line $$x = 0$$ is a vertical asimptote.
- If $$a> 1$$: $$\displaystyle \lim_{x \to 0^+} \log_ax=-\infty$$ and $$\displaystyle \lim_{x \to +\infty} \log_ax=+\infty$$
- If $$0 <1$$: $$\displaystyle \lim_{x \to 0^+} \log_ax=+\infty$$ and $$\displaystyle \lim_{x \to +\infty} \log_ax=-\infty$$
- Regularity: It is not periodic.
- Symmetries: It is not symmetric.
- Monotonicity: If $$a> 1$$, the function is strictly increasing. If $$a<1$$, the function is strictly decreasing.
- Relative extrema: It does not have any.
- Injectivity and exhaustivity: It is injective (the images of different points are different), and also it is exhaustive since the image is $$\mathbb{R}$$
