An angle is the portion of the plane determined by two half-lines with a common initial point. The half-lines that compose it are called sides of the angle and the initial point is called the vertex.
What characterizes an angle is the aperture of its sides. Therefore, we will refer to an angle when we want to talk about the aperture between two lines of any type that meet in a common point called the vertex.
Let's have a look at a drawing of an angle:
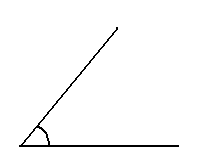
The aperture between the two half-lines is the angle.
If the sides of an angle $$a$$ are more open than those of another angle $$b$$ it is said that $$a$$ is larger than $$b$$. For example:

Given these two angles, since the aperture of the first one is larger than that of the second one, the angle $$a$$ is larger than angle $$b$$.
Note: To identify the angles, we will differentitate between two types of them.
When the angle is composed by vertexes of a polygon we will use the symbol $$\widehat{abc}$$, which means that this is the angle that form two segments $$ab$$ and $$bc$$ when the apexes $$ab$$ meet with the $$bc$$.
We can also name the angles using a Greek letter or with a number that is placed inside the angle when they are not part of any polygon. Therefore, for example:
.gif)
In this case, the blue angle is called $$\widehat{ABC}$$ since it is the one formed by the segments $$AB$$ and $$BC$$.
The green angle will be $$\widehat{BCA}$$ and the red one will be $$\widehat{CAB}$$.
For any other angle that is not part of a polygon with labeled apexes we can also use Greek letters to name it.
Let's remember that:
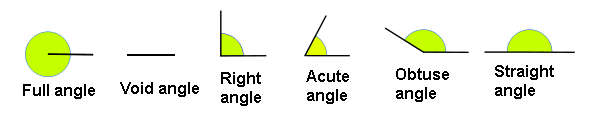
- A straightedge angle is the angle defined by two straight lines that coincide. Therefore, there is no range of rotation.
- A right angle, it is the angle defined by two perpendicular straight lines.
- A flat angle is the angle defined by two straight lines that have the same direction but opposite senses. Therefore half of it covers a semiplane, that is to say, half the plane.
- A full angle is the angle that includes the whole plane. Therefore it covers the complete plane.
- The angles smallers than a straight angle are called acute angles.
- The angles biggers than a straight angle are called obtuse angles.
Graphic representation of noteworthy angles