We will learn how to solve exercises that include questions related to the angles formed by the hands of a clock.
Let's see some practical example.
If it is three o'clock now. The clock hands make an angle of $$90^\circ$$. What will be the angle run by the hour hand $$10$$ minutes later?
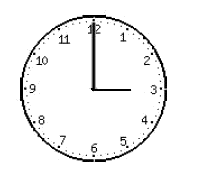
And ten minutes later it is
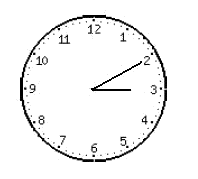
The traced angle that the minute hand has run is always $$12$$ times greater than the arc traced by the hour hand.
Thanks to this indication, we will be able to know the positions of both hands at any time.
We want to find the angle that has drawn the hour hand, which is the same as finding the arc that it has run.
Therefore, let's say that $$x$$ is the arc described by the hour hand.
The minute hand describes an arc of $$10+x$$ minutes because they ask us what angle it show $$10$$ minutes later, but the hour hand is also moving.
Bearing in mind the relation between the minute hand and the hour hand, we have: $$$10+x=12x$$$
so, $$$x=\frac {10}{11} \ \mbox{minutes}$$$
Thus, we already have the arc traced by the hour hand; it is $$$\frac{10}{11} \ \mbox{minutes}= \frac{10}{11} \ \mbox{minutes} \cdot \frac{60 \ \mbox{seconds}}{1 \ \ \mbox{minute}}= \frac{10 \cdot 60}{11} \ \mbox{seconds}= 54 \ \mbox{seconds}$$$
Understanding 54 seconds as a submultiple smaller than the degree.
Let's see another type of question about clocks.
A clock indicates $$3$$ o'clock. If we wonder at what time between $$3$$ and $$4$$ o'clock the hands will overlap, we must proceed as follows:
We call $$x$$ the arc described by the hour hand. So, $$15+x$$ will be the arc described by the minute hand, since in order to arrive at the point where the hour hand is, it must cover $$15$$ minutes from its initial starting point at $$12$$ (where the minute hand was initially when it was $$3$$ o'clock) to the point where the hour hand initially was, $$3$$ o' clock.
In this way, knowing that the traced angle that the minute hand has run is always $$12$$ times greater than the arc traced by the hour hand, the following equation is set out: $$$(15+x)=12x$$$
If we isolate the unknown $$x$$, this gives: $$$x= \frac {15}{11} \ \mbox{minutes}$$$
Therefore, the clock hands will overlap at $$3$$ and $$15+x$$ minutes, which is: $$3h \ 16 ' \ 21''$$
Let's see another example where we work on angle formed by the minute hand and the hour hand.
Our clock indicates $$2$$ o'clock. At what time will the clock hands make a right angle for the first time?
The hands of the clock will form a right angle at around $$2h \ 25'$$. We deduce this because, if we want the minute hand to form a right angle, it must point at $$15$$ minutes later than the hour indicated by the hour hand, and $$15$$ minutes later than number $$2$$ is minute $$25$$.
So, if $$x$$ is the arc that describes the hour hand, and $$25+x$$ the one that describes the minute hand, thanks to the relation that the traced angle that the minute hand has run is always $$12$$ times greater than the arc traced by the hour hand, we have: $$$25+x=12x $$$
In this case, the result that we get is: $$$ x=\frac{25}{11} \ \mbox{minutes}$$$
Therefore, the hands of the clock will form an angle of $$90^\circ$$ at $$2h$$: $$$ 25+x \ \mbox{minutes}$$$ In this case that makes: $$$2h \ 27 ' \ 16''$$$


