Two secant straight lines $$r$$ and $$s$$ determine four equal angles two by two; this is due to the fact that they are opposite angles in virtue of the apex. The smallest of the angles $$\alpha$$ and $$\beta$$ is defined as the angle between the straight lines $$r$$ and $$s$$.
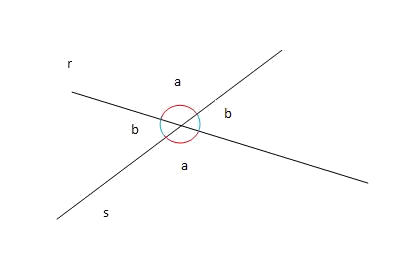
In case of the drawing, the angle between the straight lines $$r$$ and $$s$$ it would be $$\widehat{rx}=b$$.
A way of determining the above mentioned angle is from the scalar product of the director vectors of the straight lines $$r$$ and $$s$$. Let $$\overrightarrow{u}$$ and $$\overrightarrow{v}$$ be director vectors of the straight lines $$r$$ and $$s$$ respectively.
The scalar product of the vectors $$\overrightarrow{u}$$ and $$\overrightarrow {v}$$ is:$$$ \overrightarrow{u}\cdot \overrightarrow{v}=|\overrightarrow{u}||\overrightarrow{v}|\cos \widehat{(\overrightarrow{u}, \overrightarrow{v})}$$$Now, let's observe that by taking a vector director of $$r$$ and one of $$s$$, the angle formed by the above mentioned vectors coincides with the angle between both straight lines, if it is acute, or with its supplementary if it is obtuse:
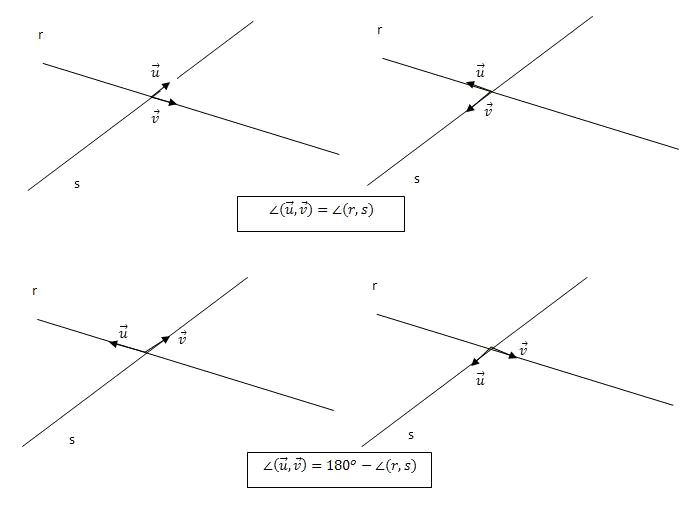
Therefore, the cosine of the angle between two straight lines will coincide, except for the sign, with that of the angle that its director vectors form, and therefore we have that:$$$\cos \widehat{(r,s)}=|\cos \widehat{(\overrightarrow{u}, \overrightarrow{v})}|$$$This last step is because $$$\cos (a) = - \cos (180 - a)$$$ This way, if we isolate in the formula of the scalar product,$$$\cos \widehat{(r,s)}=|\cos \widehat{(\overrightarrow{u},\overrightarrow{v})}|=\displaystyle \frac{|\overrightarrow{u} \cdot \overrightarrow{v}|}{|\overrightarrow{u}||\overrightarrow{v}|}$$$Note that: The scalar product between two vectors $$\overrightarrow{u}=(u_1,u_2)$$ and $$\overrightarrow{v}=(v_1,v_2)$$ is defined as $$$\overrightarrow{u} \cdot \overrightarrow{v}=u_1 \cdot v_1+u_2\cdot v_2$$$Therefore, if we remember that the expression of the module of a vector is $$$\displaystyle |\overrightarrow{v}|=\sqrt{v_1^2+v_2^2}$$$We have that in coordinates the expression of the cosine of the angle between two straight lines is:$$$\cos \widehat{(r,s)}=|\cos \widehat{(\overrightarrow{u},\overrightarrow{v})}|=\displaystyle \frac{|\overrightarrow{u} \cdot \overrightarrow{v}|}{|\overrightarrow{u}||\overrightarrow{v}|}=\frac{|u_1\cdot v_1+u_2\cdot v_2|}{\sqrt{u_1^2+u_2^2}\sqrt{v_1^2+v_2^2}}$$$
Determine the angle formed by the straight lines $$r$$ and $$s$$, which equations are, respectively, $$3x - 2y - 1 = 0$$ and $$-x + 2y - 3 = 0$$.
Let $$\overrightarrow{u}= (2, 3)$$ and $$\overrightarrow{v} = (2, 1)$$ be director vectors of the straight lines $$r$$ and $$s$$ respectively.
Then, applying the previous formula we have $$$\cos \widehat{(r,s)}=|\cos \widehat{(\overrightarrow{u},\overrightarrow{v})}|=\displaystyle \frac{|\overrightarrow{u} \cdot \overrightarrow{v}|}{|\overrightarrow{u}||\overrightarrow{v}|}=\frac{|u_1\cdot v_1+u_2\cdot v_2|}{\sqrt{u_1^2+u_2^2}\sqrt{v_1^2+v_2^2}}=$$$ $$$=\displaystyle\frac{|2 \cdot 2+ 3\cdot 1|}{\sqrt{2^2+3^2}\sqrt{2^2+1^2}}=\frac{7}{\sqrt{65}}$$$ Therefore, if we take the calculator we have $$$\widehat{rs}=\arccos(\cos (\widehat{rs}))=\arccos \Big(\displaystyle \frac{7}{\sqrt{65}}\Big)=29.7^\circ$$$
