Two straight lines on the plane can be secant, parallel or coincidental.
The following drawing shows 3 possible situations:
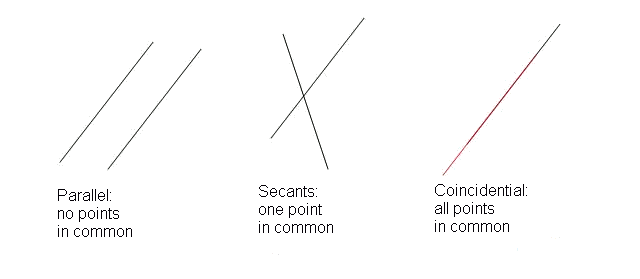
Let's see how to distinguish between these three cases. It is necessary to mention that there exist multiple ways of doing this, depending on the equation of the straight line that we have.
Obviously all of them will be equivalent and if we know how to change from one equation of the straight line to another any method of the following ones will work.
Let's see the geometric and algebraic ways of doing the problem:
From a geometric point of view, if we consider two coincidental straight lines to be a particular case of parallelism, we have two straight lines in the plane that can only be parallel or secant.
When are two straight lines parallel?
When their director vectors are parallel.
When are two vectors parallel?
When one is proportional to the other. That is, if we have the vectors $$\overrightarrow{u}$$ and $$\overrightarrow{v}$$, they must be such that $$\overrightarrow{u}=k\cdot\overrightarrow{v}$$ where $$k$$ can be any real number.
In coordinates, if $$\overrightarrow{u}=(u_1,u_2)$$ and $$\overrightarrow{v}=(v_1,v_2)$$ the vectors are proportional and therefore parallels if and only if $$$\dfrac{u_1}{v_1}=\dfrac{u_2}{v_2}$$$
Therefore, we already have a geometric way of finding the relative position of two straight lines - by seeing whether their director vectors are parallel or not:
- Parallel vector directors:
- If the straight lines have a point in common they are coincidental and they are the same.
- If the straight lines do not have any common point they are parallel.
- Non parallel director vectors: The straight lines are secant.
It is important to note that, in general, two parallel straight lines have director vectors of proportional components and equal slopes.
Consider the straight lines $$r$$ and $$s$$, which equations are respectively $$y=2x-7$$ and $$\dfrac{x-1}{3}=\dfrac{y-2}{5}$$, and find the relative position between them and, in the event that they were secant, the intersection point.
At first, we look for director vectors of both straight lines.
For $$y=2x-7$$ we have that the slope is $$m=2$$. Therefore $$\overrightarrow{u}=(1, 2)$$ is a vector director of the straight line $$r$$.
For $$\dfrac{x-1}{3}=\dfrac{y-2}{5}$$ we have $$\overrightarrow{v} = (3, 5)$$ which is a vector director of the straight line $$s$$.
Therefore, if we divide component by component we have: $$$\dfrac{u_1}{v_1}=\dfrac{1}{3}\neq\dfrac{2}{5}=\dfrac{u_2}{v_2} $$$ and therefore the director vectors are not parallel and the straight lines are secant.
We solve the system of equations formed by the equations of both straight lines to find the intersection point:
$$$\left\{\begin{array}{c} y=2x-7 \\ \dfrac{x-1}{3}=\dfrac{y-2}{5} \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} y=2x-7 \\ \dfrac{x-1}{3}=\dfrac{2x-7-2}{5} \end{array}\right. \Leftrightarrow $$$ $$$\Leftrightarrow \left\{\begin{array}{c} y=2x-7 \\ 5x-5=6x-27 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} y=2x-7 \\ x=22 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} y=37 \\ x=22 \end{array}\right.$$$
Therefore the intersection point between two straight lines is $$P = (22, 37)$$
From a more algebraic point of view, we can analyze the relative position of two straight lines $$r$$ and $$s$$, based on the number of solutions of the system of two equations that form the expressions of the straight lines $$r$$ and $$s$$.
For example, if we consider two straight lines $$r$$ and $$s$$, and their respective implicit equations:
$$\left\{\begin{array}{l} r: \ ax+by+c=0 \\ s: \ a'x+b'y+c'=0 \end{array}\right.$$
We have the system of equations:
$$\left\{\begin{array}{l} ax+by+c=0 \\ a'x+b'y+c'=0 \end{array}\right.$$
where it takes the intersection points as a solution between the straight lines $$r$$ and $$s$$. Therefore,
-
If the system has no solution, the straight lines are parallel.
-
If the system has infinite solutions, the straight lines are coincidental.
- If the system has 1 solution, the straight lines are secant.
Consider the following pairs of straight lines, and to find the relative position between them.
a) $$\left\{\begin{array}{c} -x+y=-1 \\ 2x+3y+3=0 \end{array}\right.$$
We solve the equations system: $$$\left\{\begin{array}{c} -x+y=-1 \\ 2x+3y+3=0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} -2x+2y=-2 \\ 2x+3y=-3 \end{array}\right. \Leftrightarrow \left\{\begin{eqnarray} & & -2x+2y=-2 \\ &+ & \underline{ \ \ \ 2x+3y=-3} \\ & & \ \ \ 0 \ \ +5y=-5 \end{eqnarray}\right.$$$
And the solution of the system is $$x = 0, \ y =-1$$. The fact that the solution is only one indicates to us that the straight lines are secant and the intersection point is the solution of the system.
b) $$\left\{\begin{array}{c} x+2y=2 \\ 2x+4y+1=0 \end{array}\right.$$
We solve the equations system: $$$\left\{\begin{array}{c} x+2y=2 \\ 2x+4y+1=0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} -2x-4y=-4 \\ 2x+4y=-1 \end{array}\right. \Leftrightarrow \left\{\begin{eqnarray} & & -2x-4y=-4 \\ &+ & \underline{ \ \ \ 2x+4y=-1} \\ & & \ \ \ \ \ \ \ \ 0 \ \ \ \ \ =-5 \end{eqnarray}\right.$$$
And as the system has no solution we can conclude that these two straight lines are parallel.
c) $$\left\{\begin{array}{c} -x+y=1 \\ 2x-2y=-2 \end{array}\right.$$
We solve the equations system: $$$\left\{\begin{array}{c} -x+y=1 \\ 2x-2y=-2 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} -2x+2y=2 \\ 2x-2y=-2 \end{array}\right. \Leftrightarrow \left\{\begin{eqnarray} & & -2x+2y=2 \\ &+ & \underline{ \ \ \ 2x-2y=-2} \\ & & \ \ \ \ \ \ \ \ 0 \ \ \ \ \ =0 \end{eqnarray}\right.$$$
And as the system has infinite solutions, these two straight lines have to be coincidental.
