Dada una función $$f(x)$$ definida $$$ \begin{array}{rcl} f: X & \longrightarrow &Y \\ x &\longmapsto & f(x)=y \end{array} $$$
definimos la gráfica de esta función como el conjunto de puntos: $$$ \{ (x,y)\in X\times Y \ | \ y=f(x) \} $$$ o también los pares de puntos $$(x,f(x))$$. Estos puntos se pueden representar con coordenadas cartesianas en el plano $$XY$$ formándose así el dibujo de la gráfica de la función $$f(x)$$.
Tomemos la función $$f(x)=x^3$$. Su gráfica vendrá dada por el conjunto de puntos $$ \{ (x,f(x))\}=\{(x,x^3)\} $$ variando el valor de $$x$$.
Si lo representamos obtenemos el dibujo:
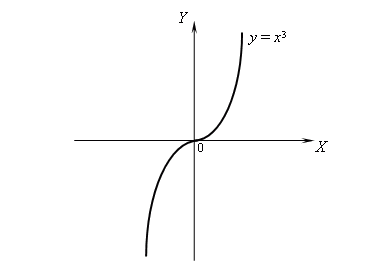
Pero, ¿Cómo se representa una gráfica? Para poder explicarlo debemos introducir antes el concepto de dominio e imagen de una función.
En una función $$f(x)$$ distinguimos dos conjuntos: uno es el conjunto de donde tomamos valores para evaluar la función (los posibles valores de $$x$$) y el otro es el conjunto formado por los diferentes valores que alcanza la función $$f(x)$$.
Entonces, definimos:
- Dominio de una función como el conjunto de valores donde evaluaremos la función. Se denota como: $$\text{Dom}(f)$$.
- Imagen de una función como el conjunto de valores obtenidos por la función. Se denota como: $$\text{Im}(f)$$.
Fijémonos que cuando notamos una función como: $$$ \begin{array}{rcl} f: X & \longrightarrow &Y \\ x &\longmapsto & f(x)=y \end{array} $$$
el conjunto $$X$$ es el dominio, puesto que tomaremos los valores de $$x$$ de dentro de éste y la imagen estaría dentro del conjunto $$Y$$.
Veámoslo mejor con algunos ejemplos:
La función $$f(x)=x$$ tiene como dominio toda la recta real, puesto que podemos evaluarla en cualquier punto, y tiene como imagen la misma recta, ya que la función es la identidad.
Por lo tanto escribiremos:
$$\text{Dom}(f)=\mathbb{R}=(-\infty,\infty)$$
$$\text{Im}(f)=\mathbb{R}=(-\infty,\infty)$$
La función té $$f(x)=x^2$$ tiene como dominio también toda la recta real (podemos evaluarla en cualquier punto) y no obstante, al ser la función "elevar al cuadrado", sólo obtenemos valores positivos. Por consiguiente su imagen será la semirecta real positiva incluyendo el cero.
Por lo tanto escribiremos:
$$\text{Dom}(f)=\mathbb{R}=(-\infty,\infty)$$
$$\text{Im}(f)=[0,\infty)$$
Podemos observar que el dominio puede ser un conjunto a elección nuestra (ya que podemos escogerlo más pequeño o más grande) mientras que la imagen vendrá dada por el dominio escogido.
A veces, pero, nos encontramos que nuestra función por ciertos motivos no puede ser evaluada en ciertos puntos ya que no está definida, así que tendremos que excluir ciertos puntos o intervalos del dominio.
Si tomamos la función $$f(x)=\dfrac{x+1}{x}+1$$ podemos ver que cuando $$x = 0$$ tenemos la expresión $$\dfrac{1}{0}$$ y esta división no puede realizarse.
Por consiguiente, el dominio de esta función será todos los reales exceptuando el cero:
$$\text{Dom}(f)=\mathbb{R}\setminus\{0\}=(-\infty,0)\cup(0,\infty)$$
Y la imagen será
$$\text{Im}(f)=\mathbb{R}\setminus\{1\}=(-\infty,1)\cup(1,\infty)$$
Cálculo de dominios:
Para calcular el dominio de una función tenemos que partir de que puede ser cualquier número de la recta real ($$\mathbb{R}$$) e ir restringiendo el conjunto dependiendo de la función. Para hacer estas restricciones debemos localizar los puntos "débiles" de nuestras funciones o mejor dicho, los puntos de no definición. A continuación listamos los conjuntos de no definición de las principales funciones:
| Función | Conjunto de no definición |
| $$f(x)=\log(g(x))$$ | $$\{x \ | \ g(x) \leqslant 0 \} =$$ los valores de $$x$$ tal que $$g(x)$$ se hace negativa o cero |
| $$f(x)=\sqrt{g(x)}$$ | $$\{x \ | \ g(x) < 0 \}=$$ los valores de $$x$$ tal que $$g(x)$$ se hace negativa |
| $$f(x)=\dfrac{g(x)}{h(x)}$$ | $$\{x \ | \ h(x)=0 \}=$$ los valores de $$x$$ tal que $$h(x)$$ vale cero |
| $$f(x)=\sqrt[2n]{g(x)}$$ | $$\{x \ | \ g(x) < 0 \}=$$ los valores de $$x$$ tal que $$g(x)$$ se hace negativa |
Si tomamos la función $$f(x)=\Big( \dfrac{2x+1}{x-4}-\ln(x+8)\Big)\cdot\sqrt{x^2+1}$$ y queremos encontrar su dominio debemos considerar que es toda la recta real y irla restringiendo según encontremos puntos o intervalos de no definición.
En este caso, observamos que tenemos 3 posibles intervalos de no definición:
- cuando $$x-4$$ sea cero $$\Rightarrow x-4=0\Rightarrow x=4 \ $$ la función no estará definida.
- cuando $$x+8$$ sea negativo o cero $$\Rightarrow x+4 \leqslant 0 \Rightarrow x\leqslant-8 \ $$ la función no estará definida.
- cuando $$x^+1$$ sea negatvo $$\Rightarrow x^2+1< 0 \Rightarrow x^2< -1 \ $$, cosa que no puede pasar ya que $$x^2$$ siempre es positivo, por lo tanto la función no tiene intervalos de no definición.
Entonces, podemos concluir que el dominio de nuestra función será: $$$ \text{Dom}(f)=(-8,4)\cup(4,\infty)$$$
Representación gráfica
Supongamos que tenemos una función $$f(x)$$. Para representarla gráficamente debemos primero encontrar su dominio para saber en que puntos debemos evaluarla.
UUna vez encontrado el dominio procederemos a hacer la representación. ¿Cómo lo haremos? Bien, la manera más simple y sencilla es mediante una tabla de valores, es decir, daremos valores a la variable $$x$$ y encontraremos el valor de $$f(x)$$ y dibujaremos el punto encontrado, $$(x,f(x))$$ en el plano usando las coordenadas cartesianas.
Tomemos la función $$f(x)=2x+1$$ y vamos a hacer la tabla de valores:
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$f(2)=2\cdot(-2)+1=-3$$ |
| $$-1$$ | $$f(2)=2\cdot(-1)+1=-1$$ |
| $$0$$ | $$f(2)=2\cdot(0)+1=1$$ |
| $$1$$ | $$f(2)=2\cdot(1)+1=3$$ |
| $$2$$ | $$f(2)=2\cdot(2)+1=5$$ |
y por lo tanto encontramos los pares de puntos:
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$-3$$ |
| $$-1$$ | $$-1$$ |
| $$0$$ | $$1$$ |
| $$1$$ | $$3$$ |
| $$2$$ | $$5$$ |
los que dibujaremos en el plano $$XY$$ y eos uniremos con una línea. Al final obtenemos:
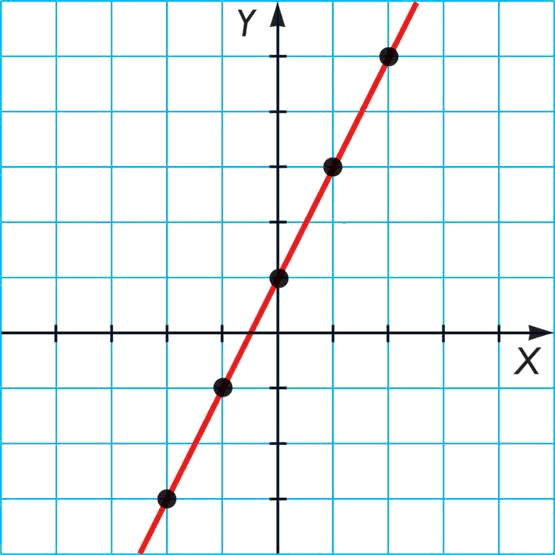
donde hemos marcado con puntos las coordenadas encontradas en la tabla de valores.
Este procedimiento (hacer la tabla de valores) puede sernos muy útil cuando debemos dibujar una función, pero a veces nos puede desconcertar, ya que existen funciones muy diversas y a veces sólo encontrando unos cuantos puntos en la tabla de valores no basta para poder dibujar la función.
