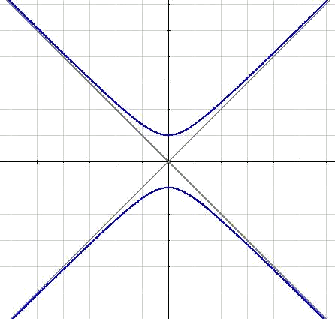
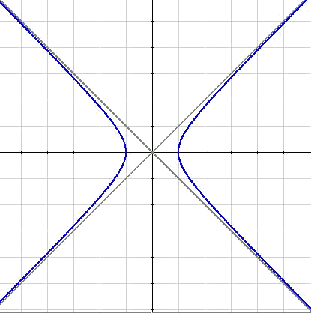
Se llama equilátera a esa hipérbola en la cual $$a=b$$. De ahí la excentricidad tiene que valer $$e=\sqrt{2}$$.
Multiplicando por $$a^2$$ en la expresión $$\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$, se llega a la ecuación $$x^2-y^2= a^2$$. En este caso las asíntotas serían $$y=x$$, $$y =-x$$.
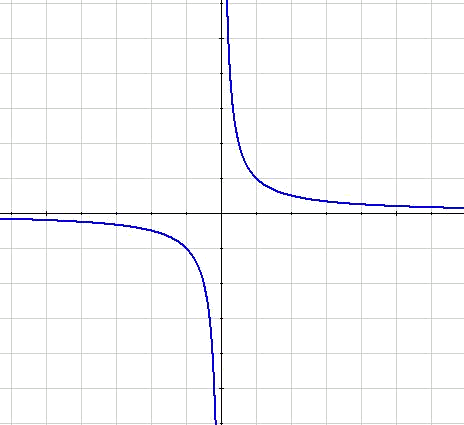
Se puede observar que las asíntotas son ortonormales. Sería entonces interesante que pudiesen coincidir con nuestros ejes ortonormales. Para llegar a ello sólo hace falta un giro de $$45^\circ$$. La ecuación resultante $$x \cdot y=\frac{a^2}{2}$$ se puede expresar de la forma $$\displaystyle y=\frac{k}{x}$$ dando lugar a la figura siguiente:
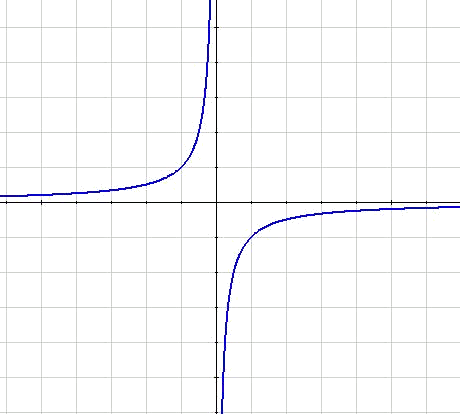
Otra expresión, en la que la hipérbola ya no estará en el primer cuadrante es $$\displaystyle y=-\frac{k}{x}$$, dando lugar a:
Dada la hipérbola $$y=-\frac{8}{x}$$, hallar su excentricidad y su distancia focal.
La excentricidad es, por definición de una hipérbola equilátera $$e=\sqrt{2}$$.
Identificar $$\displaystyle k=8=\frac{a^2}{2}$$, entonces $$a= \sqrt{16}=4$$.
Como $$a=b$$, con $$c^2=a^2+b^2$$ se encuentra $$c= \sqrt{2 \cdot a^2}=a\sqrt{2}=4\sqrt{2}$$.
