The area of an annulus can be found as the subtraction of the area of the biggest circle (radius $$R$$) minus the minor circle (radius $$r$$).
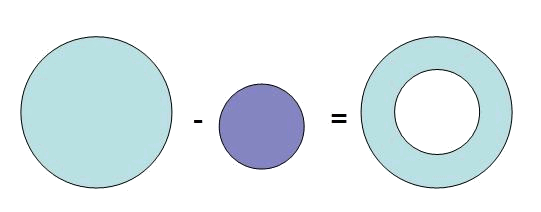
$$$A_{annulus}=A_{big \ circle}-A_{small \ circle}=\pi \cdot R^2- \pi \cdot r^2= \pi \cdot(R^2-r^2)$$$
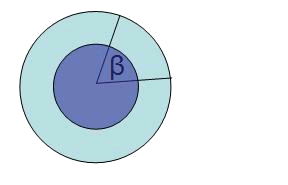
Using proportions we will find the area of a circular trapezoid, like the one in blue in the following figure:

$$$\frac{A_{circular \ trapezoid}}{A_{annulus}}=\frac{\beta_{degrees}}{360^\circ}$$$
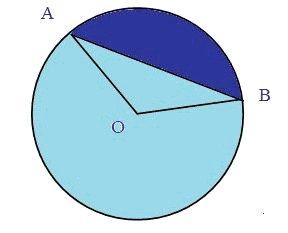
To find the area of a circular segment like the one that can be seen in the next figure, it is enough to subtract the area of the triangle $$AOB$$ and the area of the annulus.