The lune

1. Construction of the lune:

   1. We draw an isosceles rectangular triangle

   

   2. The arc of circumference $$AB$$ is created by the circle centred in $$O$$

   

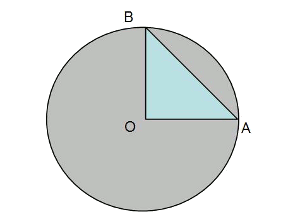
   3. We draw another arc that passes through $$AB$$, this time with the center in the middle point of the hypotenuse $$AB$$:

   

   The blue section is the lune.

2. Area of the lune:

Area of the lune = Area of the semicircle - Area of the circular segment

Area of the lune = Area of the semicircle - Area of the sector + Area of the triangle

$$$A_{lune}=\frac{\pi \cdot r^2}{2}- \frac{\pi \cdot r'^2 \cdot 90^\circ}{360^\circ}+A_{triangle}$$$

where the first $$r$$ is half of the hypotenuse of the triangle, and the second $$r$$ is the measure $$OA=OB$$.