The cone frustum is the figure resulting from having made a cut parallel to the basis of a cone.
To calculate the area of the mentioned figure we have to add up the areas of two bases and the area of the lateral face: $$$A_{total}=A_{basis}+A_{minor \ basis}+A_{lateral} \\ A_{lateral}=\pi (R+r)\cdot g$$$
In many exercises we will have the height $$h$$ of the frustum but not its $$g$$ (generatrix). The Pythagoras theorem in the triangle that appears next relates $$g$$ and $$h$$.
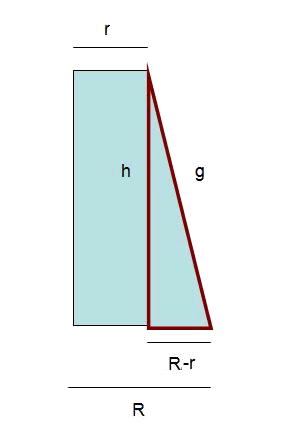
Finally, the volume of the frustum of cone is solved with the following expression: $$$V=\dfrac{1}{3}\pi \cdot h(R^2+r^2\cdot R)$$$

