Symmetric functions
As you might think, the functions can have different forms and some of them are symmetric, some are antisymmetric and others have different forms with no clear patterns.
The symmetries always depend on an axis (the mirror where the symmetry is referred to). So a symmetrical function must fulfill the following condition:
If $$f(x)$$ is a symmetric function with respect to the axis $$x=x_0$$, then it is satisfied that: $$$ f(x+x_0)=f(-x+x_0)$$$
Particularly, if we have symmetry with respect to the axis $$x=0$$, we have $$f(x)=f(-x)$$.
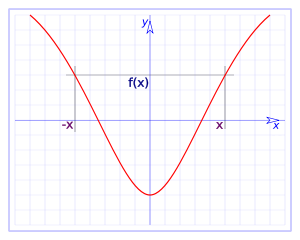
Traditionally and for general agreement, we call even function the functions that satisfy $$f(x)=f(-x)$$ (so it is symmetrical with respect to the axis $$x = 0$$).
On the other hand, we can find the antisymmetric functions, which are functions that have one kind of symmetry with respect to an axis $$x=x_0$$ but instead of performing similar to the symmetric ones, they are symmetric in an inverse way, with negative values (multiplied by $$-1$$).
These functions satisfy the condition: $$$f(x+x_0)=-f(-x+x_0)$$$
Particularly, if we have antisymmetry with respect to the axis $$x = 0$$, we have $$f(x)=-f(-x)$$.
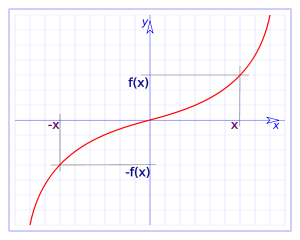
Again for general agreement, we call odd function the functions that satisfy $$f(x)=-f(-x)$$ (antisymmetry with respect to the axis $$x = 0$$).
Let's observe that the antisymmetric functions must satisfy, at some point $$x=x_0$$ that $$f(x_0)=0$$, since if $$x=0$$: $$$ f(x+x_0)=-f(-x+x_0) \Rightarrow f(x_0)=-f(x_0) \Rightarrow 2f(x_0)=0 \Rightarrow$$$ $$$\Rightarrow f(x_0)=0$$$
Let's see some examples of symmetric and antisymmetric functions:
The function $$f(x)=x^2$$ is a clear example of an even function, since $$$ f(-x)=(-x)^2=(-1)^2 x^2=x^2=f(x) $$$
The function $$f(x)=x^3$$ is an example of odd function, since $$$ f(-x)=(-x)^3=(-1)^3 x^3=-1\cdot x^3=-x^3=-f(x) $$$
The function $$f(x) = 2x-4$$ is an antisymmetric function with respect to the axis $$x = 2$$ (since $$f(2) = 0$$) and we can verify this:
$$$ f(-x+2)=2(-x+2)-4=-2x+4-4=-2x-4+4=-2(x+2)+4$$$ $$$=-(2(x+2)-4)=-f(x+2) $$$
The function $$f(x)=(x-1)^2$$ is a symmetric function with respect to $$x=1$$:
$$$f(-x+1)=(-x+1-1)^2=(-x)^2=x^2=(x+1-1)^2=f(x+1)$$$
Periodic functions
We will call periodic functions those that are repeating one part of the function.
We can say also that a periodic function will have period $$T$$ if it satisfies that:
$$$f(x+T)=f(x)$$$
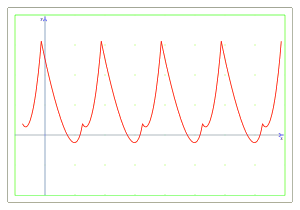
In the plot we can clearly see a periodic behavior of the function.
Let's see a few examples of periodic functions.
The function $$f(x)=c$$ where $$c$$ is a constant is periodic and with undefined period since it is a constant function.
The function $$f(x)=\sin(x)$$ is periodic and the period is $$2\pi$$, since: $$$f(x+2\pi)=\sin(x+2\pi)=sin(x)=f(x)$$$
Intersection points
When we have to plot a function, it often turns out to be very useful to know the exact point in which the function cuts both the $$X$$ and $$Y$$ axis.
To know exactly these points, we must follow this procedure:
- Intersection with the $$Y$$ axis: When the function cuts the axis $$Y$$ it means that at this $$x=0$$, so we have to look for the value of $$f(0)$$ This value will be the intersect with the $$Y$$ axis. Notice that we will only find one intersect with the $$Y$$ axis, since if there was more than one point it would not be a function. That is why we generally call this point 'the intersect'.
Let's see an example:
Let's take the function $$f(x)=x^2+x+1+e^x$$. we will look for the intersect point with the $$Y$$ axis by evaluating the function in the zero: $$$ f(0)=0^2+0+1+e^0=1+1=2$$$
Consequently we will say that the function has the point $$(0,2)$$ cutting the $$Y$$ axis at point $$2$$.
- Intersect with the $$X$$ when the function intersects the $$X$$ it means that we are on the line $$y = 0$$, so we must impose the condition $$f(x)=0$$ and solve the equation by isolating the $$x$$. It can occur that we find more than one solution. In this case we will have more than one intersection points with the $$X$$ axis.
Let's see an example:
Let's take the function $$f(x)=x^2-1$$. If we want to find the intersection points with the $$X$$ axis we must impose that $$f(x)=0$$, therefore: $$$ 0=f(x)=x^2-1 \Rightarrow x^2=1 \Rightarrow x=\pm 1$$$
and it turns out that we find two points, the $$(1,0)$$ and the $$(-1,0)$$ placed on the on the $$X$$ axis.
