We know that the derivative at a point of a function of a single variable gives us the slope of the tangent line to that function at that point. This means we know the rate of change (increase or decrease) of the function at that point.
Let's suppose we have a function $$f$$ which depends on more than one variable, for example $$f(x,y)=-x^2+2xy-y$$.
The graph of a function of two variables is a surface in a three dimensional space, and if we allow them to change we get an infinite amount of ways for them to change.
However, the partial derivatives also indicate the slope of a concrete tangent line to the surface. But before, we learn how to calculate partial derivatives. Later on you will see the purpose of this methodology.
To calculate a partial derivative of a function of several variables we have to derive with respect to one of those variables, as always, and hold the remaining variables fixed (as fixed values).
In our example $$f(x,y)=-x^2+2xy-y$$, if we want to take the partial derivative with respect to $$x$$, we hold the variable $$y$$ fixed, "a number", and we then derive a function of one variable, $$f(x)$$. Let's see:
$$-x^2$$ only depends of $$x$$, therefore its derivative is $$-2x$$.
The variable $$y$$ in the function $$2xy$$ is held fixed, a number. Let's take $$3$$ for example. If we do the following: $$2x3=6x$$, the derivative is $$6$$. Now we write $$2xy$$ as $$2yx$$ and consider $$2y$$ to be $$6$$. Thus the derivative of $$2xy=2yx$$ is $$2y$$.
And therefore $$y$$ does not contain the variable $$x$$. This means the derivative of a fixed value is $$0$$, and disappears.
Now we only need to know the correct notation to write this mathematically. To take the partial derivative of a function $$f$$ with respect to the variable $$x$$ we can establish the following notations:
$$$\dfrac{\delta f}{\delta x}$$$ $$$\delta_x f$$$ $$$f_x$$$
Thus, our partial derivative with respect to $$x$$ of $$f(x,y) =-x^2+2xy-y$$ is written as
$$$\dfrac{\delta f}{\delta x}=-2x+2y-0=2x+2y$$$ $$$\delta_x f=-2x+2y$$$ $$$f_x=-2x+2y$$$
Surely you wonder if we can also calculate the partial derivative with respect to $$y$$, don't you? Well, of course we can!
Let's calculate $$\dfrac{\delta f}{\delta y}$$, and imagine $$x$$ to be held fixed.
$$-x^2$$ doesn't contain the variable $$y$$, which means it is as if we'd have only one fixed value and its derivative is $$0$$.
$$2xy$$ contains the variable $$x$$, but it is as if it were held fixed, a number. Therefore, the derivative of $$2xy$$ is $$2x$$.
And finally, since we are deriving with respect to $$y$$, the derivative of $$y$$ is $$1$$.
Thus, $$$\dfrac{\delta f}{\delta y}=\delta_y f=f_y=2x-1$$$
Geometric interpretation of the partial derivative
But what does the calculation of a partial derivative mean geometrically? Let's look at the following example:
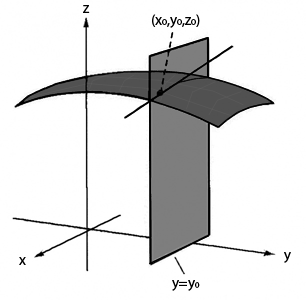
In this graph we have a surface $$z=f(x,y)$$ of which we are calculating the partial derivative with respect to the variable $$x$$ at a point $$x_0,y_0,z_0$$. We have seen that calculating a partial derivative with respect to $$x$$ means holding the variable $$y$$ fixed. Maintaining the fixed value $$y=y_0$$ results in a plane passing through point $$y_0$$. Let's draw the plane parallel to the $$x$$ axis. This plane intersects our surface. At the intersection curve we consider the tangent line at the point $$x_0,y_0,z_0$$. The partial derivative gives us the slope of this line.
If we want the value of the slope of the tangent line to the surface at the point $$3,1$$ in the direction of the axis $$x$$ in our sample function $$f(x,y)=-x^2+2xy-y$$, we get the following
$$$\dfrac{\delta f}{\delta x}=-2x+2y$$$ $$$\dfrac{\delta f(3,1)}{\delta x}=(-2)·3+2·1=-6+2=-4$$$
To graphically represent the partial derivative with respect to $$y$$ for a function $$z=f(x,y)$$, we follow this example:

Now the fixed value is $$x=x_0$$ and the plane is parallel to the axis $$y$$.
If we want to know the slope in the direction $$y$$ at the point $$(0,1)$$ of our sample function, we get
$$$\dfrac{\delta f}{\delta y}=2x-1$$$ $$$\dfrac{\delta f(0,1)}{\delta y}=-1$$$
We see that the inclination of the surface at this point and in the mentioned direction is descending.
In short, when we calculate partial derivatives $$\dfrac{\delta f} {\delta x}$$ and $$\dfrac{\delta f} {\delta y}$$ at the point $$x_0,y_0,z_0$$ the value we get is the slope of the surface in the direction of the $$x$$ or $$y$$ axis, respectively.
Formal definition of a partial derivative
As well as derivatives of functions of one variable, partial derivatives define limits.
If $$U$$ is an open subset of $$\mathbb{R}^n$$ and a function $$f: \ U \rightarrow R$$, we define the partial derivative of $$f$$ at the point $$p\in U$$, $$p=p_1,...,p_n$$, regarding the variable $$x_i$$ as
$$$\dfrac{\delta f(p)}{\delta x_i}=\lim_{h\rightarrow 0}\dfrac{f(p_1,...,p_{i-1},p_i+h,p_{i+1},...,p_n)-f(p_1,...,p_n)}{h}$$$
Examples of calculating partial derivatives
It's important to keep two things in mind to successfully calculate partial derivatives: the rules of functions of one variable and knowing to determine which variables are held fixed in each case. You will see that it is only a matter of practice.
Given the function $$f(x,y)=\sqrt{x^3+y^2}$$ calculate $$f_x(1,1)$$.
Rewrite $$f(x,y)=(x^3+y^2)^{\ frac{1}{2}}$$ as we did before to derive square roots with only one variable. Now we hold $$y$$ fixed and derive by using the usual rules
$$$f_x=\dfrac{1}{2}(x^3+y^2)^{-\frac{1}{2}}\cdot3x^2=\dfrac{3x^2}{2\sqrt{x^3+y^2}}$$$
To find the slope at the point $$(1,1)$$ we replace
$$$f_x (1,1)=\dfrac{3}{2\sqrt{2}}$$$
Given the function $$f(x,y)=\dfrac{2xy-y}{x^2+y}$$ calculate the partial derivative with respect to $$x$$ and $$y$$.
$$$\dfrac{\delta f}{\delta x}=\dfrac{2y(x^2+y)-(2xy-y)2x}{(x^2+y)^2}=\dfrac{2yx^2+2y^2-4x^2y+2xy}{(x^2+y)^2}=\dfrac{-2x^2y+2xy+2y^2}{(x^2+y)^2}=\dfrac{2(-x^2y+xy+y^2)}{(x^2+y)^2}$$$
$$$\dfrac{\delta f}{\delta y}=\dfrac{(2x-1)(x^2+y)-(2xy-y)}{(x^2+y)^2}=\dfrac{2x^3+2xy-x^2-y-2xy+y}{(x^2+y)^2}=\dfrac{2x^3-x^2}{(x^2+y)^2}$$$
Given the function $$f(x,y,z)=x^2y^3-2xyz^3$$ calculate the slope of the tangent line at the point $$(1,-1,1)$$ in the direction of the axis $$x$$, $$y$$ and $$z$$.
$$$\dfrac{\delta f}{\delta x}=2xy^3-2yz^3$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta x}=2\cdot1\cdot(-1)^3-2\cdot(-1)\cdot1^3=0$$$
$$$\dfrac{\delta f}{\delta y}=3x^2y^2-2xz^3$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta y}=3-2=1$$$
$$$\dfrac{\delta f}{\delta z}=-6xyz^2$$$ $$$\dfrac{\delta f(1,-1,1)}{\delta z}=6$$$
Given the function $$f(x,y,z)=\dfrac{2z}{y+\sin(x)}$$ calculate the partial derivatives with respect to $$x$$, $$y$$ and $$z$$.
$$$\dfrac{\delta f}{\delta x}=\dfrac{-2z\cos(x)}{(y+\sin(x))^2}$$$
$$$\dfrac{\delta f}{\delta y}=\dfrac{-2z}{(y+\sin(x))^2}$$$
$$$\dfrac{\delta f}{\delta z}=\dfrac{2(y+\sin(x))-2z\cdot0}{(y+\sin(x))^2}=\dfrac{2(y+\sin(x))}{(y+\sin(x))^2}=\dfrac{2}{y+\sin(x)}$$$
More applications of partial derivatives
At this point you might be thinking in other information partial derivatives could provide. And sure enough, we can also interpret that partial derivatives measure the rate of change of the variable we derive with respect to the variable held fixed. Like this we can measure how $$y$$ changes when we hold $$x$$ fixed and vice versa. Here's an example.
Imagine a rectangular solar panel that absorbs different amounts of sunlight depending on the area and therefore each cell produces a different amount of energy. With the following relation we can deduce the energy generated at the point $$x,y$$ of the solar panel $$$E(x,y)= \dfrac{3}{10}xy + y$$$

The units of $$x$$ and $$y$$ are centimeters and the power output $$E$$ is measured in Watts. How does the power output $$E$$ change in the center of the panel, $$(65,120)$$, when $$x$$ is held fixed at $$65$$ cm?
To find out we calculate $$E_y(65,120)$$. $$$E_y=\dfrac{3}{10}x+1 \Rightarrow E_y(65,120)=20,5$$$
So we see that at the point $$x=65$$, $$y=120$$ the power output increases as we move in the direction of axis $$y$$ since the partial derivative in this direction is positive. Besides, we also know that the generated energy increases with a rate of $$20,5$$ W.

