Introduction to fractions

A fraction is a quantity divided by another quantity. And a fractional unit is each of the parts that are obtained when dividing a unit. But to see these concepts clearly we are going to do the following construction:

We take any object, it can be a cake, a pencil, a pizza or even a table, but we are going to use a blue square:

After that, we will divide this square in four equal parts:

And we are going to paint one of them in red:

Thus, we can define the fraction that corresponds to the red part, and we will do so by saying that the red little square is the fourth part of the original blue square. So we write the fraction of the square that is red as:

$$\dfrac{1}{4}=\dfrac{\mbox{red parts of the square}}{\mbox{total parts of the square}}$$

In the same way we might consider the square in six equal parts:

And of these six, we paint four of them in red:

Then we can write the fraction of the red parts as: $$\dfrac{4}{6}=\dfrac{\mbox {red parts of the square}}{\mbox{total parts of the square}}$$

Always write the fractions like this: the number of selected parts above the line, with the total number of parts below. And to read it, first say the number above and then the number below indicating it with a divided by, namely:

one divided by two (a half) will be: $$\dfrac{1}{2}$$

three divided by ten: $$\dfrac{3}{10}$$

eleven divided by six: $$\dfrac{11}{6}$$

Furthermore, if the fraction is divided by two, we talk about a half, when divided by three we talk about a third, and when divided by four we talk about a quarter... by five a fifth, etc.:

three halves: $$\dfrac{3}{2}$$

five elevenths: $$\dfrac{5}{11}$$

seven elevenths: $$\dfrac{7}{11}$$

Let's note that the second number is the one that names the fraction indicating whether or not they are halves, thirds or eighths; for this reason we call it a denominator because it gives us the name of the fraction.

On the other hand, the first number show us the number of selected parts (coloured in red) that we have, which means that it shows us the different fractions with an equal denominator, and because of this we call it a numerator .

$$$\displaystyle \begin{array}{rcl} \underline{2} & \leftarrow & numerator \\ 3 &\leftarrow & denominator\end{array}$$$

Let's consider now the fraction represented by the following drawing:

The gray parts can be expressed as $$\dfrac{3}{5}$$ that is, three fifths. This type of expression is equivalent to the division:

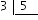
To see it clearer we start with the fraction one fifth: $$\dfrac{1}{5}$$.

As we have already seen graphically, this fraction is equivalent to cutting a rectangle in five equal parts, and taking only one of them.

So, to divide $$1$$ square in $$5$$ parts, $$\dfrac{1}{5}$$, is equivalent to doing the division

If we have three fifths: $$\dfrac{3}{5}$$, we divided the rectangle in five parts and we have taken three, that's why we do the division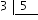

Any division can be written as a fraction, and any fraction can be written as a division, but it is important that, when writing the fractions, the numerators and the denominators are neither decimal numbers nor roots. So, the numerator and denominator must always be integers.

According to this, we might think that the number $$5$$ is not a fraction, but it is. This is so because the fraction $$\dfrac{5}{1}$$ is equivalent to the division , and if we solve it, the result is:

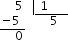
Therefore: $$$\dfrac{5}{1}=5$$$

In the same way, it is possible to assign any fraction whose denominator is $$1$$ to an integer.

Now we are prepared to give a formal definition of a fraction.

Definition: If $$a$$ and $$b$$ are two such integers where $$b\neq0$$, we call a fraction the expression $$\frac{a}{b}$$ in which $$a$$ is the numerator and $$b$$ the denominator, and all of which equals the division of $$a$$ by $$b$$.

The main use of fractions is to express parts of a whole. Let's see an example to start:

To express each part of a football game we say it is three quarters of an hour and we write $$\dfrac{3}{4}$$h.

To understand what $$\dfrac{3}{4}$$h means, we must divide the hour into four parts and take three. As we know that an hour is $$60$$ minutes, we divide $$60$$ into $$4$$, and we get $$15$$, so a fourth part of $$60$$ is $$15$$: a quarter of an hour is $$15$$ minutes.

To get what three quarters of an hour mean, we must multiply a quarter by three. Thus, $$\dfrac{3}{4}$$h are $$15\cdot3=45$$ minutes.

In general, if we want to calculate $$\dfrac{n}{m}$$ of a quantity $$x$$ (with $$m\neq0$$) we must do the following operations: $$(x:m)\cdot n$$