Consider a function $$f$$ an every element $$x$$ of the domain and its image $$y = f(x)$$. We have the pair $$(x, y)$$ (equivalent to $$(x, f(x))$$ ).
Observe the axis of coordinates of the figure. We represent in the $$x$$-axis the set of values of $$x$$ and in the $$y$$-axis the set of values of $$y = f(x)$$.
The graph of a function $$f$$ is the representation in these two axis of coordinates of all the pairs of the form $$(x, f (x))$$, being $$x$$ an element of the domain of $$f$$.
In practice it is not possible to represent all the pairs $$(x, f (x))$$, since in general they are infinite. Instead we only consider the representation of some of those points, the most representative, according to the characteristics of the given function.
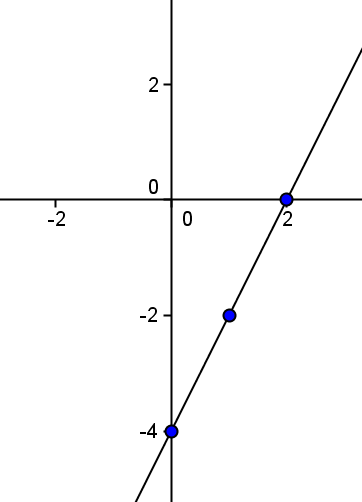
Represent graphically the function $$f (x) = 2x - 4$$.
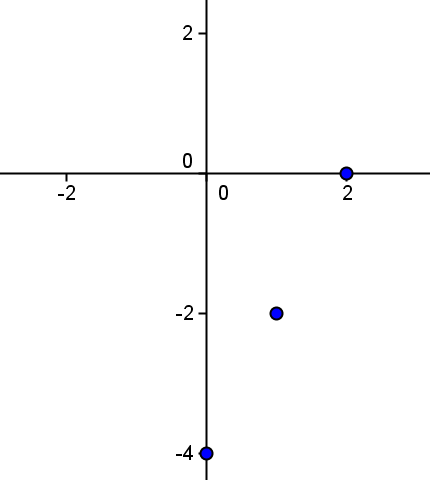
We start by constructing a table of several pairs $$(x, f (x))$$:
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$f(-2)=2 \cdot (-2)-4=-8$$ |
| $$-1$$ | $$f(-1)=2 \cdot (-1)-4=-6$$ |
| $$0$$ | $$f(0)=2 \cdot (0)-4=-4$$ |
| $$1$$ | $$f(1)=2 \cdot (1)-4=-2$$ |
| $$2$$ | $$f(2)=2 \cdot (2)-4=0$$ |
If we represent these points:
Finally, if we join them we obtain the straight line we wanted to represent:
It is important to bear in mind that, that not all the functions are continuous (for example the case of the functions defined by parts). In these cases it is necessary to indicate whether the point belong to the continuous line plotting the function or not. We will use following notation:
We will end the lines with a small dot.
- if the dot is full, it means that the point belongs to the graph of the function.
- if the circle is empty (that is, we have a small circle), it means that the point does not belong to the graph of the function.
Observe the following function defined by parts:
In the point $$x = 0$$, we have $$f (0) = 1$$.
We observe also that $$f (2)$$ is not defined, and $$f (3) = 1$$.

