Functions defined by parts

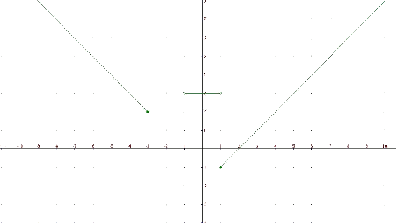
The function $$$f(x)=\left\{\begin{array}{rcl} -x-1 & \mbox{ if } & x \leq -3 \\ 3 & \mbox{ if } & -1 < x < 1 \\ x-2 & \mbox{ if } & x\geq 1 \end{array}\right.=\left\{\begin{array}{rcl} -x-1 & \mbox{ if } & x\in (-\infty,3] \\ 3 & \mbox{ if } & x\in (-1,1)\\ x-2 & \mbox{ if } & x\in [1, +\infty]\end{array}\right.$$$ It is a function defined by parts.

In the previous case for example,

• if $$x=-4$$, we substitute in $$f(x)=-x-1$$ and obtain $$f(-4)=3$$
• if $$x=-2$$, the image is not defined since $$-2$$ does not belong to any interval of the function.
• if $$x=0.5$$, we substitute in $$f(x)=3$$ obtaining $$f(0.5)=3$$
• if we $$x=1$$ substitute in $$f(X)=x-2$$ obtaining $$f(1)=-1$$

Since each of the expressions of the parts are defined in some domain, the domain of the function $$f(x)$$ is the union of the intervals of the parts of the function. $$$Dom(f)=(-\infty,-3] \cup (-1,1)\cup [1,+\infty)=(-\infty,-3]\cup (-1,+ \infty)$$$ If we look now at the graph of the previous function, we can observe that $$Im (f)=[-1,+\infty)$$:

Consider the function $$\displaystyle f(x)=\left\{\begin{array}{rcl} 1 & \mbox{ if } & x\leq 2 \\ 2 & \mbox{ if } & x > 2\end{array}\right.$$.

Its graph is the union of the graphs of the functions $$f(x)=1$$ for $$x \leq 2$$ and $$f(x)=2$$ for $$x>2$$.

The graphic representation would be:

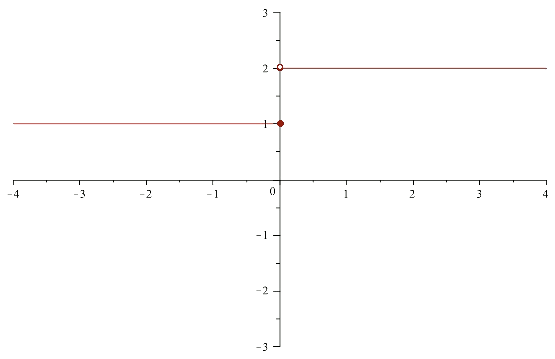
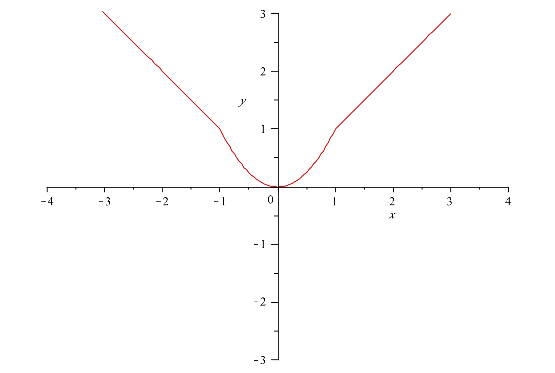
Consider the function $$\displaystyle f(x)=\left\{\begin{array}{rcl} -x & \mbox{ if } & x\leq -1 \\ x^2 & \mbox{ if } & -1 < x < 1 \\ x & \mbox{ if } & x \geq 1 \end{array}\right.$$

This time its graph will be the union of a straight line, a parable and another straight line, with each one defined where it is indicated in the definition of the function.

$$\displaystyle f(x)=\left\{\begin{array}{rcl} 2x-1 & \mbox{ if } & x < 1 \\ x+3 & \mbox{ if } & x > 1 \end{array}\right.$$

and if we want to evaluate at $$x=-1$$ in this example we will obtain:$$f(-1)=f_1(-1)=2(-1)=2(-1)-1=-2-1=-3$$

$$\displaystyle f(x)=\left\{\begin{array}{rcl} x-1 & \mbox{ if } & x<-3 \\ x^2+1 & \mbox{ if } & -3\leq < 0 \\ 3 & \mbox{ if } &0 \leq x \leq 100 \\ \ln(x+e^x) & \mbox{ if } x>100 \end{array}\right.$$

and if we want to evaluate at $$x=-1$$ in this example we will obtain: $$f(-1)=f_2(-1)=(-1)^2+1=1+1=2$$

The following example is not a function by parts since the sets of the definition are not disjoint: $$$\displaystyle f(x)=\left\{\begin{array}{rcl} x & \mbox{ if } & x < 0 \\ x+1 & \mbox{ if } & -1 < x < 2 \\ -3 & \mbox{ if } x\geq 2 \end{array}\right.$$$

since for points in $$(-1,0)$$ it would be necessary to evaluate the function at $$f_1(x)=x$$ and at $$f_2(x)=x+1$$, and thus we would obtain two different values for only one point and this would not be a function.