Constant function
This is a function of the type $$f (x) = k$$, where $$k$$ is any real number. Note that the value of $$f (x)$$ is always $$k$$, independently of the value of $$x$$.
This way, for instance, if we wanted to represent a quantity that stays constant over the course of time $$t$$, we would use a constant function $$f (t) = k$$, in which the variable $$t$$ does not appear.
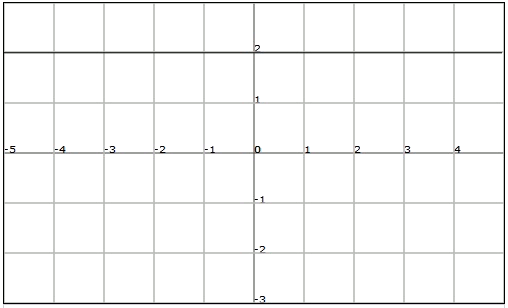
The constant functions cut through the vertical axis in the value of the constant and they are parallel to the horizontal axis (and therefore they do not cut through it).
The graph of a constant function, for example $$f (x) = 2$$, is:
Linear function
The function of a real variable that takes as a general equation $$y= mx$$, whose graph is a straight line passing through the coordinates origin, is called a linear function.
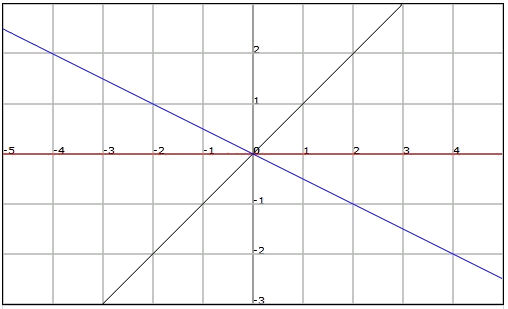
In the linear functions of this type ($$y= mx$$), the value of $$m$$, which corresponds to a real number, is called the slope. The slope measures the inclination of the line with respect to the abscissa axis.
The slope of the straight line $$y = -2x$$ is $$-2$$.
The slope of the straight line $$y = 0$$ is $$0$$.
The slope of the straight line $$y = 3x$$ is $$3$$.
It is important to understand that the larger the value of the slope $$m$$ is, the larger the inclination of the line with respect to the horizontal axis is. Also,
-
If $$m$$ is positive ($$m> 0$$), the line passes through the first and third quadrants.
-
If $$m$$ is negative ($$m <0$$), the line passes through the second and fourth quadrants.
- If $$m$$ is zero ($$m = 0$$), the line is horizontal and it coincides with the abscissa axis.
The slope of a line can also be calculated using the coordinates of a point of the line for a linear function, and from the coordinates of two points for any line.
Let's see the general way since it will also serve us well for the affine functions:
Given two points of a line (be it a linear or affine function) $$(x_1, y_1)$$ and $$(x_2,y_2)$$, we can calculate the slope of the above mentioned line by means of the expression: $$$\displaystyle m=\frac{y_2-y_1}{x_2-x_1}$$$
Considering the following line that passes through point $$(2,-1)$$:

we can calculate the slope, since in addition to point $$A$$, we know that it passes through the origin. This way, applying the formula: $$$\displaystyle m=\frac{-1-0}{2-0}=-\frac{1}{2}$$$
Affine function
The function of a real variable that takes as a general equation $$y = mx + n$$, whose graph is a straight line that does not pass through the origin (if $$n\neq 0$$), is called an affine function.
As in the previous case, $$m$$ is the slope of the straight line.
It is also worth mentioning that the cutting point of an affine function $$f (x) = mx + n$$ with the axis of ordinates is point $$(0, n)$$.
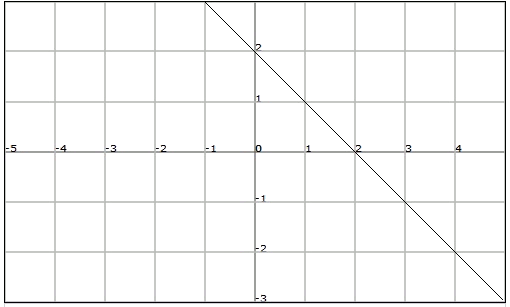
An example of affine function is $$f (x) = -x +2$$
Consider the following functions, and determine of which type they are, at what point they cut through the axis of ordinates, and the abscissa, and what their slopes are.
- $$f (x) = 2$$
- $$f (x) = 2x$$
-
$$f (x) = 2x +2$$
- This is a constant function. Its slope is $$0$$ and therefore it is parallel to the abscissa axis. It cuts through the vertical axis at $$(0,2)$$.
- This is a linear function. Its slope is $$2$$. It cuts through both axes at point $$(0,0)$$.
- This is an affine function. Its slope is $$2$$. It cuts through the vertical axis at point $$(0, 2)$$, and the horizontal axis at $$(-1, 0)$$ (we do $$y = 0 = 2x + 2$$ and solve).

